We know that velocity in string is given by
\(\mathrm{v}=\sqrt{\frac{\mathrm{T}}{\mu}}\) \(...(I)\)
where \(\mu=\frac{\mathrm{m}}{1}=\frac{\text { mass of string }}{\text { length of string }}\)
The tension \(\mathrm{T}=\frac{\mathrm{m}}{\ell} \times \mathrm{x} \times \mathrm{g}\) \(...(II)\)
From \((a)\) and \((b)\)
\(\frac{d x}{d t}=\sqrt{g x}\)
\(\mathrm{x}^{-1 / 2} \mathrm{dx}=\sqrt{\mathrm{g}} \mathrm{dt} \quad \therefore \int_{0}^{\ell} \mathrm{x}^{-1 / 2} \mathrm{dx}-\sqrt{\mathrm{g}} \int_{0}^{\ell} \mathrm{dt}\)
\(2 \sqrt{l}=\sqrt{g} \times t \quad \therefore t=2 \sqrt{\frac{\ell}{g}}=2 \sqrt{\frac{20}{10}}=2 \sqrt{2}\)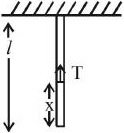
Download our appand get started for free
Similar Questions
- 1એક પ્રગામી પ્રસંવાદી તરંગને સમીકરણView Solution
$y(x, t) = 10^{-3}\,sin\,(50t + 2x)$
વડે રજુ કરવામાં આવે છે, જ્યાં $x$ અને $y$ એ મીટરમાં અને $t$ એ સેકન્ડમાં છે. આ તરંગ માટે નીચેમાંથી કયું વિધાન સાચું છે?
- 2$ {y_1} = 5\sin 2\pi (75t - 0.25x) $ અને $ {y_2} = 10\sin 2\pi (150t - 0.50x) $ તરંગની તીવ્રતાનો ગુણોત્તર $ \frac{I_1}{I_2}=$View Solution
- 3સમાન આવૃત્તિ અને વેગ ધરાવતા બે તરંગોનો કંપવિસ્તાર $2A$ અને $A$ છે.બંને તરંગ એક જ દિશામાં સમાન કળામાં ગતિ કરતાં હોય,તો પરિણામી કંપવિસ્તાર કેટલો થાય?View Solution
- 4બે તરંગોના સમીકરણો $x_1=a \sin \left(\omega t+\phi_1\right)$ અને $x_2=a$ $\sin \left(\omega t+\phi_2\right)$ છે. જો પરિણામી તરંગની આવૃતિ અને કંપવિસ્તાર સંપાત પામતા તરંગો જેટલી જ રહે, તો તેમની વચ્ચેનો કળા તફાવત કેટલો હોય.View Solution
- 5બે તરંગો નીચેના સમીકરણોથી દર્શાવી શકાય છે. $y_1 = a \,sin\, \omega t $ અને $y_2 = a\, cos\, \omega t$ પ્રથમ તરંગ એ .....View Solution
- 6View Solutionસમાન લંબાઈની ખુલ્લી નળી અને બંધનળીમાં ઉત્પન્ન થતા મૂળભૂત હાર્મોનિકની આવૃત્તિઓનો ગુણોત્તર શું થાય?
- 7View Solutionનીચેનામાંથી કયું તરંગનું સમીકરણ છે?
- 8બે સમાન વાંસળી $300Hz$ મૂળભૂત આવૃત્તિ $ {27^o} C$ તાપમાને ઉત્પન્ન કરે છે,એક વાંસળીનું $ {31^o} C$ તાપમાન કરવાથી કેટલા સ્પંદ ઉત્પન્ન થાય?View Solution
- 9એક સબમરીનમાં રાખેલી સોનાર $(SONAR)$ પદ્ધતિ $40.0\, kHz$ પર કાર્યાન્વિત થાય છે. એક દુશ્મન સબમરીન $SONAR$ તરફ $360\, km\, h^{-1}$ ની ઝડપથી ગતિ કરી રહી છે. બીજી સબમરીનથી પરાવર્તિત થતા ધ્વનિતરંગની આવૃત્તિ કેટલી હશે ? પાણીમાં ધ્વનિની ઝડપ $1450\, m\,s^{ -1}$ લો.View Solution
- 10પ્રગામી તરંગનું સમીકરણ $y = 0.2\cos \pi \left( {0.04t + 0.02x - \frac{\pi }{6}} \right)\, cm$ હોય,તો $ \pi /2 $ ના કળા તફાવતે રહેલા બે બિંદુ વચ્ચેનું અંતર કેટલું .... $cm$ હશે?View Solution
