$50\, cm$ અને $50.5\, cm$ ની સમાન ઓપન પાઇપને ધ્વનિત કરાવવામાં આવે ત્યારે પ્રતિ સેકન્ડે $3$ સ્પંદ સંભળાય છે. તો હવામાં ધ્વનિની ઝડપ($m/s$ માં) કેટલી હશે?
Medium
Download our app for free and get started
a
\(L_{1}=50 \mathrm{cm}, L_{2}=50.5 \mathrm{cm}\)
\(L_{1}=50 \mathrm{cm}, L_{2}=50.5 \mathrm{cm}\)
as \(L_{2}>L_{1},\) so \(n_{2}\)
For open pipe,
\(n=\frac{v}{2 L}\)
\(n_{1}-n_{2}=3\) beats \(/ \mathrm{s}\)
\(\frac{v}{2}\left(\frac{1}{L_{1}}-\frac{1}{L_{2}}\right)=3\)
\(\frac{v}{10^{-2}}\left(\frac{1}{50}-\frac{1}{50.5}\right)=6\)
\(v=\frac{6 \times 50 \times 50.5 \times 10^{-2}}{0.5}=303 \mathrm{m} / \mathrm{s}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સ્વરકાંટો અને $95 cm$ અથવા $100 cm$ ના સોનોમીટરનો તારને સાથે કંપન કરાવતાં $4$ સ્પંદ પ્રતિ સેકન્ડ સંભળાય છે. તો સ્વરકાંટાની આવૃત્તિ કેટલી ..... $Hz$ થાય?View Solution
- 2નિચેનામાંથી ક્યું વિધેય $y$ માટે કદી પ્રસ્તુત તરંગ દર્શાવી ન શકે ?View Solution
$(a)$ $\left(x^2-v t\right)^2$
$(b)$ $\log \left[\frac{(x+v t)}{x_0}\right]$
$(c)$ $e^{\left\{-\frac{(x+v t)}{x_0}\right\}^2}$
$(d)$ $\frac{1}{x+v t}$
- 3તરંગનું સમીકરણ $Y = 7 \,sin \,\left( {7\pi \,t\, - 0.04\pi x\; + \,\frac{\pi }{3}} \right)$ હોય,તો તરંગની ઝડપ કેટલી ...... $m/sec$ થાય?View Solution
- 4બે સ્વરકાંટાને એકસાથે કંપન કરાવતા $6$ સ્પંદ પ્રતિ સેકન્ડે સંભળાય છે,એક સ્વરકાંટાની આવૃત્તિ $256$ છે.બીજા સ્વરકાંટાને મીણ લગાવતાં સ્પંદની સંખ્યા $6$ પ્રતિ સેકન્ડ થાય છે,તો બીજા સ્વરકાંટાની આવૃત્તિ કેટલી ..... $Hz$ થાય?View Solution
- 5સ્વરકાંટો $250\, {Hz}$ થી કંપન કરે છે. સ્વરકાંટા સાથે અનુનાદ કરવા માટે ક્લોઝ પાઇપની લઘુતમ લંબાઈ કેટલા ${cm}$ હોવી જોઈએ?View Solution
(હવામાં ધ્વનિની ઝડપ $340\, {ms}^{-1}$)
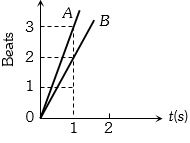
- 6સ્વરકાંટા $P$ અને $Q$ ને સાથે કંપન કરાવતા ઉત્પન્ન થતાં સ્પંદ $OA$ રેખા દ્વારા દર્શાવવામાં આવે છે, $Q$ પર મીણ લગાવાથી ઉત્પન્ન થતાં સ્પંદ $OB$ રેખા દ્વારા દર્શાવવામાં આવે છે,જો $P$ ની આવૃત્તિ $341 Hz$ હોય,તો $Q$ ની આવૃત્તિ કેટલી ... $ Hz$ થાય?View Solution
- 7એક તરંગને $Y =10^{-2} \sin 2 \pi(160 t-0.5 x+\pi / 4)$,વડે રજૂ કરવામાં આવે છે, જ્યાં $x$ અને $Y$ મીટરમાં અને $t$ સેકન્ડમાં છે. તરંગની ઝડપ .......... $km\,h ^{-1}$ હશે.View Solution
- 8View Solutionએક ચોક્કસ સમયે સ્થિત લંબગત તરંગ મહત્તમ ગતિઉર્જા ધરાવે છે. આ સમયે દોરીની સ્થિતિ શું હશે?
- 9એક લંબગત તરંગ $y=2 \sin (\omega t-k x) cm$ વડે રજૂ થાય છે. જ્યારે તરંગવેગ કણના મહત્તમ વેગ જેટલો થાય તે માટે તરંગલંબાઈનું મૂલ્ય $...........cm$ થશે.View Solution
- 10અવલોકનકાર ધ્વનિના વેગના $1/5^{th}$ વેગથી સ્થિર ઉદ્ગમ તરફ ગતિ કરે છે. ઉદ્ગમ દ્વારા ઉત્પન્ન થતા ધ્વનિની તરંગલંબાઇ અને આવૃતિ અનુક્રમે $ \lambda $ અને $f$ છે. અવલોકનકારને સંભળાતી આભાસી આવૃત્તિ અને તરંગલંબાઇ કેટલી હશે?View Solution