$60$ $cm$ લંબાઇ ધરાવતો એક ગેનાઇટનો સળિયો તેનાં મધ્યબિંદુ આગળથી જડિત કરી તેમાં સંગત $(loggitudinal )$ દોલનો પ્રસ્થાપિત કરવામાં આવે છે.ગ્રેનાઇટની ઘનતા $2.7 \times 10^3 $ $kg/m^3$ અને તેનો યંગ મોડયુલસ $9.27 \times 10^{10}$ $Pa$ છે.આ સંગત તરંગોની મૂળભૂત આવૃત્તિ કેટલી ... $kHz$ હશે?
JEE MAIN 2018, Difficult
d
In solids, Velocity of wave \(V=\sqrt{\frac{Y}{\rho}}=\sqrt{\frac{9.27 \times 10^{10}}{2.7 \times 10^{3}}}\)
In solids, Velocity of wave \(V=\sqrt{\frac{Y}{\rho}}=\sqrt{\frac{9.27 \times 10^{10}}{2.7 \times 10^{3}}}\)
\(\mathrm{v}=5.85 \times 10^{3} \mathrm{m} / \mathrm{sec}\)
since rod is clamped at middle fundamental wave shape is as follow
\(\frac{\lambda}{2}=\mathrm{L} \Rightarrow \lambda=2 \mathrm{L}\)
\(\lambda=1.2 \mathrm{m}(\because \mathrm{L}=60 \mathrm{cm}=0.6 \mathrm{m}(\mathrm{given})\)
Using \(v=f \lambda\)
\(\Rightarrow \quad f=\frac{v}{\lambda}=\frac{5.85 \times 10^{3}}{1.2}\)
\(=4.88 \times 10^{3} \mathrm{Hz}=5 \mathrm{KHz}\)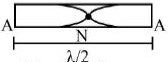
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બંદૂકનો અવાજ ગોળી છોડયા પછી $8 sec$ પછી સંભળાતો હોય,તો પરાવર્તક સપાટી કેટલા ....$m$ અંતરે હોય? (હવામાં ધ્વનિની ઝડપ $= 350\, m/s$)View Solution
- 2હવામાં ધ્વનિની ઝડપ $330\, m/sec$ છે. હવામાં કોઈ વિશેષ ધ્વનિનો $40\;cm$ પથ તફાવત $1.6 \pi $ કળા તફાવતને બરાબર છે. આ તરંગની આવૃત્તિ ($Hz$ માં) કેટલી થાય?View Solution
- 3ઘન $x- $ દિશામાં ગતિ કરતું તરંગ $ y = A\sin (\omega t - kx) $ છે,તો $B$ બિંદુ આગળ મહત્તમ ઢાળ કેટલો થાય?View Solution

- 4ભૂકંપમાં લંબગત $(S)$ અને સંગત તરંગ $(P)$ ઉત્પન્ન થાય છે, $S$ અને $P $ તરંગની ઝડપ $4.5\, km/sec$ અને $8.0 \,km/sec$ છે, $P$ તરંગ એ $S$ તરંગ કરતાં $4$ મિનિટ વહેલાં નોંધાય તો, ભૂકંપનું કેન્દ્ર સિસ્મોગ્રાફથી કેટલા .... $km$ અંતરે હોય $?$View Solution
- 5સોનોમીટર વાયરની આવૃતિ $100\,Hz$ છે. વજન દ્વારા ઉત્પન થતા તણાવને પાણીમાં ડુબાડવામાં આવે તો આવૃત્તિ $80\,Hz$ છે અને ચોક્સસ પ્રવાહીમાં ડુબાડવામાં આવે તો $60\,Hz$ છે. પ્રવાહીનો વિશિષ્ટ ગુરુત્વાકર્ષણ $..............$View Solution
- 6બે વિરુદ્ધ દિશામાં ગતિ કરતાં તરંગના સંપાતીકરણથી સ્થિત તરંગ બને છે. લંબગત સ્થાનાંતર $y\left( {x,t} \right) = 0.5\sin\, \left( {\frac{{5\pi }}{4}x} \right)\,\cos\, \left( {200\,\pi t} \right)$ મુજબ આપવામાં આવે છે. ધન $x-$દિશામાં ગતિ કરતાં તરંગનો વેગ ($m/s$માં) કેટલો મળે? ($x$ અને $t$ મીટર અને સેકન્ડમાં છે)View Solution
- 7એક બાઇક પાછળ પોલિસની કાર $22 m/s$ ની ઝડપથી જઇ રહી છે.પોલીસની કાર દ્રારા $176 Hz $ આવૃતિ ઘરાવતો હોર્ન વગાડવામાં આવે છે. બંને એક $165 Hz$ ઘરાવતા સાઇરન તરફ ગતિ કરી રહયા છે.જો બાઇક સવારને સ્પંદ અનુભવાતા ન હોય તો બાઇકની ઝડપ ... $m/s$ કેટલી હશે? (હવામાં ઘ્વનિની ઝડપ $330 m/s$ )View Solution

- 8અનુનાદિત સ્તંભ માટે અંતિમ કરેક્શન $1\,cm$ છે. જો સ્વરકાંટાની ઓછામાં ઓછી $10\,cm$ લંબાઈ સાથે તે અનુનાદ કરતો હોય તો બીજી અનુનાદિત લંબાઈ કેટલા $cm$ હશે?View Solution
- 9$1.5 m$ લંબાઇની બંધ પાઇપની ત્રીજી આવૃત્તિ કેટલી ... $Hz$ થાય? હવામાં ધ્વનિનો વેગ $330 m/s$ છે.View Solution
- 10એક મોટી દીવાલની સામે ગતિ કરતાં એક બસનો ડ્રાઇવર ધરાવતા બસના હોર્નને જ્યારે સાંભળે અને પછી જ્યારે તે દીવાલ સાથે અથડાયને પછી આવે ત્યારે તેની આવૃતિ $420\, Hz$ થી $490\, Hz$ બદલાય છે. જો હવામાં ધ્વનિની ઝડપ $330\, ms ^{-1}$ હોય તો બસની ઝડપ ($kmh^{-1}$ માં) કેટલી હશે?View Solution
