\(\mathrm{n}_{\mathrm{A}}=425 \mathrm{Hz}, \mathrm{n}_{\mathrm{B}}=?\)
Beat frequency \(x=5\) \(Hz\) which is decreasing \((5 \rightarrow 3)\) after increasing the tension of the string \(B\).
Also tension of string \(\mathrm{B}\) increasing so
\(\mathrm{n}_{\mathrm{B}} \uparrow(\because \mathrm{n} \propto \sqrt{\mathrm{T}})\)
Hence \(\quad \mathrm{n}_{\mathrm{A}}-\mathrm{n}_{\mathrm{B}} \uparrow=x \downarrow \longrightarrow\) correct
\(\mathrm{n}_{\mathrm{B}} \uparrow-\mathrm{n}_{\mathrm{A}}=\mathrm{x} \downarrow \longrightarrow \text { incorrect }\)
\(\therefore \mathrm{n}_{\mathrm{B}}=\mathrm{n}_{\mathrm{A}}-\mathrm{x}=425-5=420 \mathrm{Hz}\)
Download our appand get started for free
Similar Questions
- 1હવાના કણોનું સ્થાનાંતર $(s)$ એ ધ્વનિના તરંગ દ્વારા ઉત્પન્ન થતાં દબાણના તફાવત $(\Delta p)$ ના સમપ્રમાણમાં છે. સ્થાનાંતર $(s)$ એ ધ્વનિની ઝડપ $(v),$ હવાની ઘનતા $(\rho)$ અને આવૃતિ $(f)$ પર પણ આધાર રાખે છે. જો $\Delta p \approx 10\, Pa , v \approx 300\, m / s , p \approx 1\, kg / m ^{3}$ અને $f \approx 1000 \,Hz$ હોય તો $s$ નું મૂલ્ય કયા ક્રમનું હશે?View Solution
(ગુણકારનો અચળાંક $1$ લો)
- 2સોનોમીટરના તારની લંબાઈ $0.75\;m$ અને ઘનતા $9 \times 10^3\;Kg / m ^3$ છે. તે સ્થિતિસ્થાપક હદ ઓળંગવા સિવાય $8.1\times 10^8 \;N / m ^2$ નો તણાવ સહન કરી શકે છે. આ તારમાં ઉત્પન્ન કરી શકાતી મુળભુત આવૃતિ કેટલી હોય?View Solution
- 3$A$ અને $B$ બે સ્ત્રોત અવાજના તરંગો ઉત્પન્ન કરે છે. શ્રોતા $C$ બિંદુ આગળ છે. $A$ બિંદુ આગળ સ્ત્રોતની આવૃતિ $500\,Hz$ છે. $A$ હવે $4\,m/s$ ના વેગથી $C$ તરફ ગતિ કરે છે. $C$ બિંદુ આગળ $6$ સ્પંદ સંભળાય છે. જ્યારે $A$, $C$ થી $4\,m/s$ ના વેગથી દૂર જાય છે ત્યારે $C$ ને $18$ સ્પંદ સંભળાય છે. જો ધ્વનિનો ઝડપ $340\,m/s$ હોય તો $B$ સ્ત્રોત આગળ આવૃતિ $Hz$ માં કેટલી હશે?View Solution

- 4જ્યારે બે અવાજના તરંગને એક જ માધ્યમમાં સમાન દિશામાં ગતિ કરતાં હોય તેના માટે સમીકરણ નીચે મુજબ આપવામાં આવે છેView Solution
${y_1} = 0.05\,\cos \,\left( {0.50\,\pi x - 100\,\pi t} \right)$
${y_2} = 0.05\,\cos \,\left( {0.46\,\pi x - 92\,\pi t} \right)$
તો તેનો વેગ $m/s$માં કેટલો મળે?
- 5$51.6 \;cm $ અને $49.1 \;cm$ લંબાઇ ધરાવતા બે તારના છેડે અલગથી $20\; N$ જેટલું બળ લગાડેલ છે. બંને તારનું એકમ લંબાઇ દીઠ દળ સમાન અને $1\; g/m $ ને બરાબર છે. જ્યારે બંને તારને એકસ્થે કંપન કરાવવામાં આવે, તો સ્પંદની સંખ્યા કેટલી હશે?View Solution
- 6બે સ્વરકાંટાને એકસાથે કંપન કરાવતા $5$ સ્પંદ પ્રતિ સેકન્ડે સંભળાય છે,એક સ્વરકાંટાની આવૃત્તિ $512$ છે. બીજા સ્વરકાંટાને મીણ લગાવતાં સ્પંદની સંખ્યા વધે છે, તો બીજા સ્વરકાંટાની આવૃત્તિ કેટલી થાય?View Solution
- 7ધ્વનિ-ચીપિયાને એક $288 \,cps$ ના ચીપિયા સાથે કંપિત કરતાં $4$ સ્પંદ પ્રતિ સેકન્ડે ઉત્પન્ન કરે છે. બીજા અજ્ઞાત ચીપિયા પર થોડું મીણ લગાડતાં $2$ સ્પંદ સંભળાય છે, તો આ અજ્ઞાત ચીપિયાની આવૃત્તિ ($cps$ માં) કેટલી કેટલી હશે?View Solution
- 8$450 Hz$ આવૃત્તિવાળા ઉદ્ગમ સ્થિર અવલોકનકાર તરફ $33\, m/s$ વેગથી ગતિ કરતો હોય તો કેટલી આવૃત્તિ સંભળાય? (હવામાં ધ્વનિનો વેગ $332 \,m/s$ છે.)View Solution
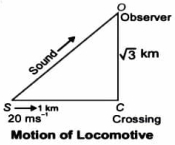
- 9ક્રોસિંગ નજીક પહોંચતી ટ્રેનની ઝડ૫ $20 \,ms ^{-1}$ છે. તે જ્યારે ક્રોસિંગથી $1 \,km$ દુર હોય ત્યારે $640 \,Hz$ આવૃતિની સીટી વગાડે છે. હવા શાંત છે અને હવામાં અવાજની ઝડપ $330\,ms ^{-1}$ છે. ક્રોસિંગથી લંબ રીતે $\sqrt{3} \,km$ દૂર ઉભેલા શ્રોતા વડે ........ $Hz$ આવૃતિ સંભળાશે.View Solution
- 10$L$ લંબાઇ અને $M$ દળ ધરાવતું એક દોરડું શિરોલંબ લટકાવીને તેના નીચેના છેડે તરંગ ઉત્પન્ન કરતા તે $ \;x $ અંતર કાપે ત્યારે તેનો વેગ કોના સપ્રમાણમાં હોય?View Solution
