(c) Suppose two tuning forks are named \(A\) and \(B\) with frequencies \({n_A} = 256\,Hz\) (known), \(n_B = ?\) (unknown), and beat frequency \(x = 4 \,bps.\)
Frequency of unknown tuning fork may be \({n_B} = 256 + 4 = 260\,Hz\)
or \( = 256 - 4 = 252\,Hz\)
It is given that on sounding waxed fork \(A\) (fork of frequency \(256 Hz\)) and fork \(B\), number of beats (beat frequency) increases.
It means that with decrease in frequency of \(A,\) the difference in new frequency of \(A\) and the frequency of \(B\) has increased.
This is possible only when the frequency of \(A\) while decreasing is moving away from the frequency of \(B.\)
This is possible only if \(n_B = 260 Hz.\)
Alternate method : It is given \({n_A} = 256\,Hz,\,{n_B} = ?\) and \(x = 4 \,bps\)
Also after loading \(A\) (i.e. \(n_A \downarrow\)), beat frequency (i.e. \(x\)) increases (\(\uparrow\)).
Apply these informations in two possibilities to known the frequency of unknown tuning fork.
\(n_A \downarrow -n_B = x\uparrow\) ... \((i)\)
\(n_B -n_A \downarrow = x\uparrow\) ... \((ii)\)
It is obvious that equation \((i)\) is wrong \((ii)\) is correct so
\(n_B = n_A + x = 256 + 4 = 260 \,Hz.\)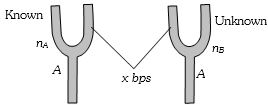
Download our appand get started for free
Similar Questions
- 1$S_1$ અને $S_2$ બે ધ્વનિ ઉદગમો સમાન આવૃતિ $660\, Hz$ ઉત્પન્ન કરે છે.સાંભળનાર $S_1$ ઉદગમથી $S_2$ ઉદગમ તરફ $u\, m/s$ જેટલા અચળ વેગથી ગતિ કરે છે અને તેને $10$ સ્પંદ સંભળાય છે.હવામાં ધ્વનિની ઝડપ $330\, m/s$ હોય તો $u$ કેટલો ... $m/s$ હશે?View Solution
- 2કોઈ એક નિશ્ચિત ઓર્ગન પાઈપ માટે ત્રણ અનુક્રમિત આવૃતિઓ $425,595$ અને $765 \,Hz$ છે. હવામાં અવાજની ઝડપ $340 \,m / s$ હોય. તો પાઈપની મુળભુત આવૃતિ ($Hz$ માં) કટલી હશે.View Solution
- 3$f$ આવૃતિવાળી સિસોટી $S$ એ $R$ ત્રિજ્યાના વર્તુળ પર અચળ ઝડપ $v$ થી ભ્રમણ કરે છે. તો કેન્દ્રથી $2R$ અંતરે રહેલા સ્થિર ડિટેક્ટર $D$દ્વારા મપાતી મહતમ અને લઘુત્તમ આવૃતિનો ગુણોત્તર કેટલો થાય?View Solution
($c=$ હવામાં ધ્વનિનો વેગ)
- 4$108 km/hr$ ની ઝડપથી ગતિ કરતી બે ટ્રેન એકબીજાને ક્રોસ કરે છે, એક ટ્રેન $750 Hz$ નો હોર્ન વગાડતાં, ટ્રેન ક્રોસ થયા પછી બીજી ટ્રેનમાં રહેલ માણસને કેટલી ... $Hz$ આવૃત્તિ સંભળાશે? (હવામાં ધ્વનિનો વેગ $330 m/s$ છે.)View Solution
- 5...... $^oC$ તાપમાને હાઇડ્રોજનમાં ધ્વનિની ઝડપ $ 100^oC $ તાપમાને રહેલા ઓકિસજનમાં ધ્વનિની ઝડપ જેટલી થાય?View Solution
- 6$27\, km/hr$ ની ઝડપથી જતી સબમરીન $(B)$ $18\, km/hr$ની ઝડપથી જતી સબમરીન $(A)$ નો પીછો કરે છે.$B$ $A$ ને શોધવા $500\, Hz$ નું સોનાર સિગ્નલ મોકલે છે અને $v$ આવૃતિનો અવાજ મેળવે છે.તો $v$ ની કિમત કેટલી ... $Hz$ હશે? (પાણીમાં ધ્વનિની ઝડપ $= 1500\, ms^{-1}$)View Solution
- 7બંદૂકનો અવાજ ગોળી છોડયા પછી $8 sec$ પછી સંભળાતો હોય,તો પરાવર્તક સપાટી કેટલા ....$m$ અંતરે હોય? (હવામાં ધ્વનિની ઝડપ $= 350\, m/s$)View Solution
- 8$X-$ દિશામાં પ્રસરણ પામતા તરંગનું તરંગ -સમીકરણ નીચે મુજબ છે.$y\left( {x,t} \right) = 0.005cos\left( {\alpha x - \beta t} \right)$જો તરંગની તરંગલંબાઇ અને આવર્તકાળ અનુક્રમે $0.08$ $m$ અને $2.0$ $s$ હોય,તો $\alpha $ અને $\beta $ નાં મૂલ્યો યોગ્ય એકમમાં કેટલા હશે?View Solution
- 9$20$ ધ્વનિ ચીપીયાઓના ગણને તેમની આવૃત્તિના ચઢતા ક્રમમમાં ગોઠવવામાં આવેલ છે. જો દરેક ચીપીયો તેની આગળના ચીપીયા સાથે $4$ સ્પંદ આપતો હોય અને છેલ્છેલા ચીપીયાની આવૃત્તિ એ પ્રથમ ચીપીયાની આવૃત્તિ કરતા બમણી હોય તો, છેલ્લા ચીપીયાની આવૃત્તિ ........... $Hz$ થશે.View Solution
- 10બંને છેડેથી જડિત $10 \,m$ લાંબી દોરીમાં સ્થિત તરંગ ઉત્પન્ન કરવામાં આવે છે. જો દોરી $5$ વિભાગમાં દોલન કરે છે અને તરંગની ઝડપ $20\,m / s$, છે. તો આવૃતિ .............. $Hz$ હોય.View Solution
