દોરીમાં તણાવ $69\%$ વધારતાં, આવૃત્તિ અચળ રાખવા માટે લંબાઇમાં કેટલો $\%$ .... વધારો કરવો પડે?
Medium
Download our app for free and get started
b
(b) \(n \propto \frac{{\sqrt T }}{l}\)\( \Rightarrow l \propto \sqrt T \) (As \(n\)= constant)
(b) \(n \propto \frac{{\sqrt T }}{l}\)\( \Rightarrow l \propto \sqrt T \) (As \(n\)= constant)
==>\(\frac{{{l_2}}}{{{l_1}}} = \sqrt {\frac{{{T_2}}}{{{T_1}}}} = {l_1}\sqrt {\frac{{169}}{{100}}} \Rightarrow {l_2} = 1.3{l_1} = {l_1} + 30\% \) of \({l_1}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1કારની છત પરથી $m$ દળવાળી હલકી દોરી વડે એક $M$ દળવાળા ભારે દડાને લટકાવવામાં આવે છે $(m < < M)$.જ્યારે કાર સ્થિર હોય ત્યારે દોરી પર રચાતા લંબગત તરંગોની ઝડપ $60\ ms^{-1}$ છે. જ્યારે કાર $a$ જેટલા પ્રવેગથી પ્રવેગીત થાય છે ત્યારે તરંગ ઝડપ વધીને $60.5\ ms^{-1}$ થાય છે. ગરૂત્વીય પ્રવેગ $g $ ના પદમાં $a$ નું મૂલ્ય_____ની નજીકનું હશેView Solution
- 2$X-$ દિશામાં પ્રસરણ પામતા તરંગનું તરંગ -સમીકરણ નીચે મુજબ છે.$y\left( {x,t} \right) = 0.005cos\left( {\alpha x - \beta t} \right)$જો તરંગની તરંગલંબાઇ અને આવર્તકાળ અનુક્રમે $0.08$ $m$ અને $2.0$ $s$ હોય,તો $\alpha $ અને $\beta $ નાં મૂલ્યો યોગ્ય એકમમાં કેટલા હશે?View Solution
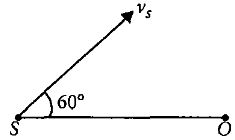
- 3$100\; Hz$ આવૃત્તિનો ધ્વનિ ઉત્પન્ન કરતો ધ્વનિ સ્ત્રોત $S$ તથા અવલોકનકાર $O$ એ એકબીજાથી અમુક અંતરે સ્થિર છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે ધ્વનિ ઉદ્ગમ $19.4\; ms^{-1}$ ઝડપથી ઉદ્ગમ અને અવલોકનકારના સ્થાનને જોડતી સીધી રેખા સાથે $ 60^o $ ના ખૂણે ગતિ કરે છે. અવલોકનકાર સ્થિર છે. અવલોકનકાર દ્વારા સંભળાતા ધ્વનિની આભાસી આવૃત્તિ ($Hz$ માં) કેટલી હશે? (હવામાં ધ્વનિનો વેગ $330\; ms^{-1}$ છે.)View Solution
- 4એક હૉસ્પિટલમાં પેશીમાંની ગાંઠ (ગ્રંથિ)નું સ્થાન નક્કી કરવા અલ્ટ્રાસોનિક સ્કેનર વપરાય છે. જો ગાંઠમાં ધ્વનિની ઝડપ $1.7\, km s^{-1}$ હોય તેમાં ધ્વનિની તરંગલંબાઈ કેટલી હશે? સ્કેનરની કાર્યવાહક (Operating) આવૃત્તિ $4.2\, MHz$ છે.View Solution
- 5બંધ પાઇપની મૂળભૂત આવૃત્તિ $50\,Hz$ હોય,તો $2^{nd}$ ઓવરટોનની આવૃતિ કેટલી .... $Hz$ થાય?View Solution
- 6જ્યારે અવાજનું ઉદગમ સ્થિર શ્રોતા તરફ $V_s$ ઝડપે ગતિ કરે છે ત્યારે તેની આવૃતિમાં $10 \%$ નો વધારો થાય છે. જો ઉદગમ સમાન ઝડપથી શ્રોતાથી દૂર જાય તો આવૃતિમાં ....... $\%$ ટકાનો ફેરફાર થાય. $\left(V_s < V\right)$View Solution
- 7$105 \,cm$ લંબાઈની બંધ ઓર્ગન પાઈપમાં ત્રીજો ઓવરટોન દર્શાવતો સ્થિત તરંગ ઉત્પન્ન કરવામાં આવ્યો છે. બંધ છેડેથી .............. $cm$ દૂર દબાણ નિસ્પંદ રચાય છે?View Solution
- 8ક્ષિતિજને સમાંતર $8 \,m$ ત્રિજ્યાના વર્તુળાકાર માગંમાં એક દોલિત સ્વરકાંટો ધીમેથી સમાાન રીતે ગતિ કરે છે. સ્વરકાંટાથી શ્રોતાનું એ જ સમતલમાં ટૂંકામાં ટુંકુ અંતર $9 \,m$ છે. જ્યારે આભાસી આવૃતિ મહત્તમ બને ત્યારે શ્રોતા અને સ્વરકાંટા વચ્ચેનુ અંતર ........ $m$ હશે.View Solution
- 9નિચેનામાંથી ક્યું વિધેય $y$ માટે કદી પ્રસ્તુત તરંગ દર્શાવી ન શકે ?View Solution
$(a)$ $\left(x^2-v t\right)^2$
$(b)$ $\log \left[\frac{(x+v t)}{x_0}\right]$
$(c)$ $e^{\left\{-\frac{(x+v t)}{x_0}\right\}^2}$
$(d)$ $\frac{1}{x+v t}$
- 10સ્થિર તરંગનું સમીકરણ $ y = 5\sin \,\left( {\frac{{2\pi x}}{3}} \right)\,\,\cos \,20\,\pi \,t \, cm $ હોય,તો બે નિસ્પંદ બિંદુ વચ્ચે કેટલું ... $cm$ અંતર હશે?View Solution