એક અવાજનું ઉદગમ શ્રોતા તરફ અવાજની ઝડપ કરતાં $(1/10)$ ગણી ઝડપે ગતિ કરે છે. આભાસી અને વાસ્તવિક આવૃતિનો ગુણોત્તર કેટલી હોય.
Easy
Download our app for free and get started
a
(a)
(a)
\(f=f_0 \frac{v}{v-v_s}\)
\(f=f_0 \frac{v}{v-v / 10}\)
\(f=\frac{10 f_0}{9}\)
\(\therefore f: f_0=\frac{10}{9}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionસંગત તરંગ માધ્યમમાંથી પસાર થાય, ત્યારે પ્રસરણની દિશામાં શેનું વહન થાય?
- 2એક સ્ત્રોત અને અવલોકનકાર એકબીજાથી જમીનની સાપેક્ષે $10\; m/s$ ના વેગથી દૂર જાય છે. જો અવલોકનકારને સ્ત્રોતમાંથી આવતા ધ્વનિની આવૃતિ $1950 \;Hz$ જેટલી સંભળાટિ હોય તો સ્ત્રોતની સાચી આવૃતિ કેટલા $Hz$ હશે? (ધ્વનિની હવામાં ઝડપ$=340 \;m/s$)View Solution
- 3સમાન આવૃત્તિ ધરાવતાં તરંગની તીવ્રતા $1 \,bel$ અને $5\, bel$ હોય,તો કંપવિસ્તારનો ગુણોત્તર કેટલો થાય?View Solution
- 4$500 Hz$ આવૃત્તિવાળો ઉદ્ગમ $30 m/s$ ના વેગથી સ્થિર અવલોકનકાર તરફ ગતિ કરે છે.અવલોકનકારને સંભળાતી આવૃત્તિ કેટલી .... $Hz$ થાય? (હવામાં ધ્વનિની ઝડપ =$ 330 ms^{-1}$)View Solution
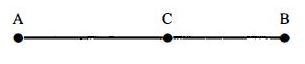
- 5$A$ અને $B$ બે સ્ત્રોત અવાજના તરંગો ઉત્પન્ન કરે છે. શ્રોતા $C$ બિંદુ આગળ છે. $A$ બિંદુ આગળ સ્ત્રોતની આવૃતિ $500\,Hz$ છે. $A$ હવે $4\,m/s$ ના વેગથી $C$ તરફ ગતિ કરે છે. $C$ બિંદુ આગળ $6$ સ્પંદ સંભળાય છે. જ્યારે $A$, $C$ થી $4\,m/s$ ના વેગથી દૂર જાય છે ત્યારે $C$ ને $18$ સ્પંદ સંભળાય છે. જો ધ્વનિનો ઝડપ $340\,m/s$ હોય તો $B$ સ્ત્રોત આગળ આવૃતિ $Hz$ માં કેટલી હશે?View Solution
- 6બે સ્વરકાંટાની આવૃત્તિ $450\,Hz$ અને $454\, Hz$ છે.તેને સાથે કંપન કરાવતાં મહત્તમ તીવ્રતા વચ્ચેનો સમય કેટલો ... $sec$ થાય?View Solution
- 7દોરી પરના લંબગત હાર્મેનિક તરંગને $y(x, t)=5 \sin (6 t+0.003 x)$ વડે રજૂ કરવામાં આવે છે, જ્યાં $x$ અને $y$ $cm$ માં અને $t$ સેકન્ડમાં છે. તરંગનો વેગ $..........\,ms^{-1}$ છે.View Solution
- 8$100$ સેમી લંબાઈનાં સ્ટીલના સળિયાને મધ્યબિંદુ એ લટકાવેલ છે, તેમાં ઉત્પન્ન થતાં સંગત કંપનની મૂળભૂત આવૃતિ $2.53\,kHz$ છે, તો સ્ટીલમાં ધ્વનિની ઝડપ ($km/s$ માં) કેટલી હશે?View Solution
- 9ગિટારનો તાર $440\, Hz$ ના આવૃતિવાળા સ્વરકાંટા સાથે $5\, Hz$ આવૃતિવાળા સ્પંદ ઉત્પન્ન કરે છે. જ્યારે $437\,Hz$ ના આવૃતિવાળા સ્વરકાંટા સાથે $8\, Hz$ આવૃતિવાળા સ્પંદ ઉત્પન્ન કરે છે. તો તારની આવૃતિ ($(Hz)$ માં) હશે?View Solution
- 10જ્યારે અવાજનું ઉદગમ સ્થિર શ્રોતા તરફ $V_s$ ઝડપે ગતિ કરે છે ત્યારે તેની આવૃતિમાં $10 \%$ નો વધારો થાય છે. જો ઉદગમ સમાન ઝડપથી શ્રોતાથી દૂર જાય તો આવૃતિમાં ....... $\%$ ટકાનો ફેરફાર થાય. $\left(V_s < V\right)$View Solution