એક કાર્નોટ એન્જિન કે જેની ઠારણ વ્યવસ્થા $300 \,K$ છે તે $50 \%$ કાર્યક્ષમતા ધરાવે છે તો પ્રાપ્તિસ્થાનનું .......... $K$ તાપમાન વધારવું જોઈએ કે જેથી તેની કાર્યક્ષમતા $70 \%$ જેટલી થાય ?
Medium
d
(d)
(d)
(d)
Temperature of sink; \(T_2=300 K\)
Original efficiency; \(\eta=50 \%=0.5\)
Let initial temperature \(: \rightarrow T_1\)
we know; \(\eta=1-\frac{T_2}{T_1}\)
Substituting the values we get:
\(0.5=1-\frac{300}{T_1}\)
\(\Rightarrow T_1=600\,K\)
Now; new efficiency; \(\eta^{\prime}=70 \%=.7\)
New initial temperature \(=T_1^{\prime}\)
\(\Rightarrow 0.7=1-\frac{T_2}{\left(T_1\right)^{\prime}}\)
\(\Rightarrow 0.7=1-\frac{300}{\left(T_1\right)^{\prime}}\)
\(\Rightarrow\left(T_1\right)^{\prime}=1000\,K\)
\(\therefore\) Increase in source temperature is:
\(\Delta T =(1000-600)\,K\)
\(\Rightarrow \Delta T =400\,K\)
So the temperature of the source should be increased by \(400\,K\).
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે સમાન દળ ધરાવતો વાયુ તાપીય સંતુલનમાં છે. જો તેના દબાણ ${P_a},\,{P_b}$ અને કદ ${V_a}$ અને ${V_b}$ છે તો તેમની વચ્ચેનો સાચો સંબંધ કયો થાય?View Solution
- 2$72cm$ મરકયુરી દબાણે રહેલા વાયુનું કદ $1 liter$ છે.તેને સમતાપી સંકોચન કરીને કદ $900 cm^3$ કરવાથી તેનું દબાણમાં ........ $cm$ (mercury) વધારો થશે?View Solution
- 3ફ્રિજની અંદરનું તાપમાન $ - 13^\circ C. $ છે.તેનો પરફોમન્સ ગુણાંક $5$ છે.તો બહાર ફેંકાતી હવાનું તાપમાન કેટલુ હશે?View Solution
- 4કાર્નોટ એન્જિન પહેલા $200^{\circ}\,C$ અને $0^{\circ}\,C$ વચ્ચે કાર્ય કરે છે અને પછી $0^{\circ}\,C$ અને $-200^{\circ}\,C$ વચ્ચે કાર્ય કરે છે. બંને કિસ્સામાં તેમની કાર્યક્ષમતાનો ગુણોત્તર $...............$View Solution
- 5$ {V_0} $ કદે રહેલા વાયુનું તાપમાન $ {27^o}C. $ છે.અચળ દબાણે વાયુનું કદ $ 2{V_0}. $ કરવાથી નવું તાપમાન કેટલું થશે?View Solution
- 6View Solutionથર્મોડાયનેમિક તંત્ર માટે નીચે પૈકી કયું વિધાન સાચું પડે?
- 7$1$ મોલ $N _{2}$ વાયુને $300\, K$ તાપમાન થી $600\, K$ તાપમાન સુધી સમદાબ પ્રક્રિયાથી ગરમ કરતા વાયુની એન્ટ્રોપીમાં ($J/K$ માં) કેટલો ફેરફાર થાય?View Solution
- 8જો સમોષ્મી પ્રક્રિયા માટે $\gamma = 2.5$ તથા કદ તેના પ્રારંભીક કદ કરતા $1/8 $ ગણું હોય તો દબાણ $P' =.... $ (પ્રારંભીક દબાણ $= P$)View Solution
- 9$STP$ એક લિટર હવાનું સમોષ્મી વિસ્તરણ થઈ તેનું કદ $3$ લિટર થાય છે.જો $\gamma=1.40,$ હોય તો હવા દ્વારા કેટલું કાર્ય થયું હશે?View Solution
$(3^{1.4}=4.6555)$ [હવાને આદર્શ વાયુ લો]
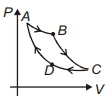
- 10કાર્નોટ ચક્ર $P-V$ આલેખમાં દોરેલ છે. ક્યો ભાગ સમતાપી પ્રસરણ રજૂ કરે છે ?View Solution