$P V^2=R T$ સમીકરણને અનુસરતા એક વાસ્તવિક વાયુ માટે અયળ દબાણે વિશિષ્ટ ઉષ્મા. . . . . . .હશે.
JEE MAIN 2024, Diffcult
d
\(\mathrm{dQ}=\mathrm{du}+\mathrm{dW}\)
\(\mathrm{dQ}=\mathrm{du}+\mathrm{dW}\)
\(\mathrm{CdT}=\mathrm{C}_{\mathrm{V}} \mathrm{dT}+\mathrm{PdV}\) \(....(1)\)
\(\therefore \quad \mathrm{PV}^2=\mathrm{RT}\)
\(\quad \mathrm{P}=\text { constant }\)
\(\quad \mathrm{P}(2 \mathrm{VdV})=\mathrm{RdT}\)
\(\quad \mathrm{PdV}=\frac{\mathrm{RdT}}{2 \mathrm{~V}}\)
Put in equation \((1)\)
\(\mathrm{C}=\mathrm{C}_{\mathrm{V}}+\frac{\mathrm{R}}{2 \mathrm{~V}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionઉષ્મા એન્જિનની મહત્તમ શક્ય કાર્યક્ષમતા કેટલી છે ?
- 2$2$ મોલ વાયુનું તાપમાન $340 \;K$ થી $342\; K$ કરતાં આંતરિકઊર્જામાં થતો વધારો ........ $cal.$ ${C_v} = 4.96\,cal/mole\,K$,View Solution
- 3પ્રતિવર્તી એન્ઝિનની કાર્યક્ષમતા $\frac{1}{4}$ છે. જો ઠારણ વ્યવસ્થાનું તાપમાન $58^{\circ} {C}$ જેટલું ઘટાડવામાં આવે તો, તેની કાર્યક્ષમતા બમણી થાય છે. તો ઠારણ વ્યવસ્થાના તાપમાનની ($^{\circ} {C}$ માં) ગણતરી કરો.View Solution
- 4ગેસ અચળ દબાણ $10^{3} Nm^{2}$ એ $0.25m^{3}$ જેટલો વિસ્તરણ પામે છે તો થતું કાર્ય....?View Solution
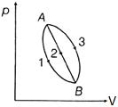
- 5$m$ દળનો આદર્શ વાયુ $A$ અવસ્થામાંથી $B$ અવસ્થાનાં ત્રણ જુદા જુદા માર્ગે ગતિ કરે છે.$Q_{1}, Q_{2}$ અને $Q_{3}$ દરેક પ્રક્રિયાના શોષણ થતી ઉષ્મા હોય તો,View Solution
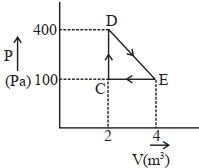
- 6એક થર્મોડાયનેમિક તંત્ર ચક્રિય પ્રક્રિયા કરે છે. પ્રક્રિયામાં થતું કુલ કાર્ય $...............\,J$ છે.View Solution
- 7View Solutionવાયુની આંતરિક ઊર્જા કોના પર આધારિત છે?
- 8પાણીના ઠારણબિંદુ અને ઉત્કલનબિંદુ વચ્ચે કાર્ય કરતાં એક આદર્શ ઉષ્માયંત્રની કાર્યક્ષમતા ($\%$ માં) કેટલી થાય?View Solution
- 9એક કિલોમોલ વાયુનું સમોષ્મી સંકોચન કરવા માટે $146 kJ $ કાર્ય કરવામાં આવે છે. આ પ્રક્રિયા દરમિયાન વાયુનું તાપમાન $7 °C$ જેટલું વધે છે. આ વાયુ ........ છે.View Solution
- 10એક આદર્શ ઉષ્મીય યંત્ર માટે, સ્ત્રોતનું તાપમાન $127\,^{\circ} C$ છે. $60\, \%$ જેટલી કાર્યક્ષમતા મેળવવા માટે, ઠારણનું તાપમાન $........\,{ }^{\circ} C$ હોવું જોઈએ. (નજીકત્તમ પૂર્ણાકમાં લખો)View Solution
