તરંગનું સમીકરણ $y = {10^4}\sin (60t + 2x).$ જ્યાં $x$ અને $y$ એ મીટર અને $t$ એ સેકન્ડમાં છે.
IIT 1982, Medium
d
(d) On comparing the given equation with
(d) On comparing the given equation with
\(y = a\sin (\omega \,t + kx),\) it is clear that wave is travelling in negative \(x-\)direction.
It's amplitude \(a = 10^4\, m\) and \(\omega = 60, k = 2.\)
Hence frequency \(n = \frac{\omega }{{2\pi }} = \frac{{60}}{{2\pi }} = \frac{{30}}{\pi }Hz\)
\(k = \frac{{2\pi }}{\lambda } = 2\) ==> \(\lambda = \pi \,m\) and \(v = \frac{\omega }{k} = \frac{{60}}{2} = 30\,m/s\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે ઉદ્રગમ $A$ અને $B$ $660 \,Hz$ આવૃતિવાળો અવાજ ઉત્પન કરે છે. શ્રોતા અચથ વેગ $u$ સાથે $A$ થી $B$ તરફ ગતિ કરે છે. જો અવાજની ઝડપ $330\, m / s$ હોય તો એક સ્કન્ડમાં $8$ સ્પંદ સાંભળવા માટે $u$ ની કિંમત ........ $m / s$ હોવી જોઈએ.?View Solution
- 2View Solutionજે તરંગ દ્વારા માધ્યમના કણોનું સ્થાનાંતર તરંગની પ્રસરણ દિશાને લંબ થતું હોય,તેને કયાં તરંગો કહે છે.
- 3બંને છેડેથી જડિત $10 \,m$ લાંબી દોરીમાં સ્થિત તરંગ ઉત્પન્ન કરવામાં આવે છે. જો દોરી $5$ વિભાગમાં દોલન કરે છે અને તરંગની ઝડપ $20\,m / s$, છે. તો આવૃતિ .............. $Hz$ હોય.View Solution
- 4બે સ્વરકાંટાને એકસાથે કંપન કરાવતા $6$ સ્પંદ પ્રતિ સેકન્ડે સંભળાય છે,એક સ્વરકાંટાની આવૃત્તિ $341$ છે.બીજા સ્વરકાંટાને મીણ લગાવતાં સ્પંદની સંખ્યા $2$ પ્રતિ સેકન્ડ થાય છે,તો બીજા સ્વરકાંટાની આવૃત્તિ કેટલી થાય?View Solution
- 5દોરીમાં તણાવ $69\%$ વધારતાં, આવૃત્તિ અચળ રાખવા માટે લંબાઇમાં કેટલો $\%$ .... વધારો કરવો પડે?View Solution
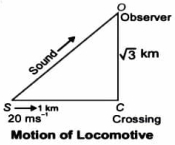
- 6ક્રોસિંગ નજીક પહોંચતી ટ્રેનની ઝડ૫ $20 \,ms ^{-1}$ છે. તે જ્યારે ક્રોસિંગથી $1 \,km$ દુર હોય ત્યારે $640 \,Hz$ આવૃતિની સીટી વગાડે છે. હવા શાંત છે અને હવામાં અવાજની ઝડપ $330\,ms ^{-1}$ છે. ક્રોસિંગથી લંબ રીતે $\sqrt{3} \,km$ દૂર ઉભેલા શ્રોતા વડે ........ $Hz$ આવૃતિ સંભળાશે.View Solution
- 7એક દોરીને $75 \;cm$ અંતરે રહેલા બે નિયત બિંદુુ વચ્ચે બાંધેલી છે. તેની અનુનાદ આવૃત્તિઓ $420\; Hz$ અને $315 \;Hz$ છે, આ બંને વચ્ચેની બીજી કોઈ આવૃત્તિ નથી. તો આ દોરી માટે સૌથી નીચેની અનુનાદ આવૃત્તિ ($Hz$ માં) કેટલી હશે?View Solution
- 8સ્વરકાંટો $250\, {Hz}$ થી કંપન કરે છે. સ્વરકાંટા સાથે અનુનાદ કરવા માટે ક્લોઝ પાઇપની લઘુતમ લંબાઈ કેટલા ${cm}$ હોવી જોઈએ?View Solution
(હવામાં ધ્વનિની ઝડપ $340\, {ms}^{-1}$)
- 9$0.5 m$ લંબાઇ અને $2 \times 10^{-4} kg$ દળ ધરાવતી દોરીમાં તણાવ $20N$ હોય,તો દ્વિતીય આવૃત્તિ કેટલી .... $Hz$ થાય?View Solution
- 10View Solutionનીચેનામાંથી કયું સમીકરણ પ્રગામી તરંગ દર્શાવે છે ?
