$0.1\, kg$ અને $0.4\, kg$ દળના બે પદાર્થો એકબીજા તરફ અનુક્રમે $1\, m/s$ અને $0.1\, m/s$ વેગથી ગતિ કરે છે. સંઘાત પછી તેઓ એકબીજા સાથે ચોંટી જાય છે. તો $10\, sec$ માં સંયુક્ત દળ કેટલા ............. $\mathrm{m}$ અંતર કાપશે?
AIIMS 2010, Medium
d
According to conservation of momentum
According to conservation of momentum
\({m_1}{v_1} + {m_2}{v_2} = \left( {{m_1} + {m_2}} \right)\,v,\)
where \(v\) is common velocity of the two bodies.
\(\begin{array}{l}
{m_1} = 0.1\,kg\,{m_2} = 0.4\,kg\\
{v_1} = 1\,m/s,\,{v_2} = - \,0.1\,m/s,\\
\therefore 0.1 \times 1 + 0.4 \times \left( { - 0.1} \right) = \left( {0.1 + 0.4} \right)v\\
or\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,01. - 0.04 = 0.5\,v,\\
v = \frac{{0.06}}{{0.5}} = 0.12\,m/s
\end{array}\)
Hence, distance covered \(= 0.12\) \( \times \,10 = 1.2\,m.\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
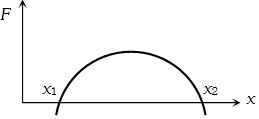
- 1$x$ -અક્ષની સાપેક્ષ પર ગતિ કરી રહેલાં એક પદાર્થ પર લાગતાં બળએ સ્થિતિ $x$ સાથે આકૃતિમાં દર્શાવ્યા મુજબ બદલાય છે. પદાર્થ ક્યારે સ્થિર સંતુલિત સ્થિતિમાં હશે?View Solution
- 2$300 g $ દળના પદાર્થનો વેગ $(3\hat i + 4\hat j)m/sec$ હોય,તો ગતિઊર્જા.....$J$View Solution
- 3$5 \,kg $ ના બ્લોક અને સપાટી વચ્ચેનો ઘર્ષણાંક $ 0.2 $ છે,તેના પર $25\, N$ નું બળ દ્વારા $ 10 \,m $ ખસેડતાં તે ...... $J$ ગતિઊર્જા પ્રાપ્ત કરશે. $ (g = 10 \,ms^2)$View Solution
- 4$m$ દળનાં એક કણને $u$ ઝડપે જમીનના સમક્ષિતિજ સાથે $\theta$ કોણે પ્રક્ષેપિત કરવામાં આવે છે. તેની ઊર્ધ્વગતિ દિશામાં ગતિ દરમિયાન ગુરુત્વાકર્ષણ વડે થયેલ કાર્ય કેટલું હશે?View Solution
- 5જ્યારે $5$ ગણું દળ ધરાવતા સ્થિર કણ સાથે ગતિ કરતો કણ અથડાય ત્યારે ગતિ કરતા કણની કેટલા પ્રતિશત ગતિઊર્જા સ્થિર કણમાં રૂપાંતરીત થશે? (ધારો કે સંધાત સ્થિતિ સ્થાપક છે.)View Solution
- 6એક $M = 4\,m$ દળ ધરાવતો ઢાળ(wedge) ઘર્ષણરહિત સમતલ પર છે. $m$ દળ ધરાવતો કણ $v$ વેગથી ઢાળ તરફ ગતિ કરે છે કણ અને સપાટી અને કણ અને ઢાળ વચ્ચેની સપાટી ઘર્ષણરહિત છે તો કણ ઢાળ(wedge) પર મહત્તમ કેટલી ઊંચાઈ સુધી ચડી શકે?View Solution
- 7$Y-$ દિશામાં ગતિ કરતા એક પદાર્થ પર $\overrightarrow F = ( - 2\hat i + 15\hat j + 6\hat k)\,N$ બળ લગાવવામાં આવે છે. $Y-$ અક્ષ પર પદાર્થને $10\, m$ ખસેડવા માટે બળ દ્વારા થયેલ કાર્ય ($J$ માં) કેટલું હશે?View Solution
- 8એક $m$ દળનો પદાર્થ $r$ ત્રિજ્યાના વર્તૂળમાં $V$ જેટલી સમાન ઝડપથી ગતિ કરે છે. $m V^2/r$ જેટલું બળ પદાર્થના કેન્દ્ર પર સીધું જ લાગે છે. આ બળ દ્વારા જ્યારે પદાર્થ વર્તૂળના પરિઘનું અડધું અંતર કાપે તે દરમિયાન પદાર્થ દ્વારા થતું કાર્ય શોધો.View Solution
- 9$m $ દળના સાદા લોલક સાથે $m$ દળ અને $v_0$ વેગથી ગતિ કરતો કણ ચોંટી જાય છે.તો ગોળો કેટલી મહત્તમ ઊંચાઇ પ્રાપ્ત કરશે?View Solution
- 10એક એલીવેટર $0.4 m/s $ ની અચળ ઝડપ સાથે $500 kg$ વજનને ઉંચકે છે. તેમાં વપરાયેલ મોટર ઓછામાં ઓછા કેટલા......$H.P.$ હોર્સ પાવરની હશે ?View Solution
