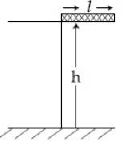
$0.3\, m$ લંબાઈ ધરાવતા એક લંબચોરસ ઘન બોક્સ સમક્ષિતિજ એક $5\,m$ લંબાઈના પ્લેટફોર્મ પર દર્શાવ્યા પ્રમાણે પડેલ છે. જ્યારે તેને મુક્ત કરવામાં આવે છે તે $ 0.01\, s$ ટૂંકા સમયમાં ટેબલ પરથી સરકે છે પરંતુ તે સમક્ષિતિજ જ રહે છે.જ્યારે તે જમીન સાથે અથડાય ત્યારે તે કેટલાના ખૂણે ($radians$ માં) ભ્રમણ કરે

JEE MAIN 2019, Diffcult
a
\(Angular \,impulse = change\, in\, angular\, momentum.\)
\(Angular \,impulse = change\, in\, angular\, momentum.\)
\(\tau \,\Delta t = \Delta L\)
\(mg\frac{\ell }{2} \times 0.01 = \frac{{m{\ell ^2}}}{3}\omega \)
\(\omega = \frac{{3g \times 0.01}}{{2\ell }} = \frac{{3 \times 10 \times 0.01}}{{2 \times 0.3}} = \frac{1}{2} = 0.5\,rad/s\)
Time taken by rod to hit the ground
\(t\sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2 \times 5}}{{10}}} = 1\,\sec .\)
In this time angule rotate by rod
\(\theta = \omega t = 0.5 \times 1 = 0.5\,radian\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
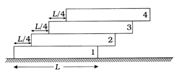
- 1આકૃતિમાં દર્શાવ્યા પ્રમાણે ચાર સમાન દળનાં પુસ્તકોને ગોઠવવામાં આવ્યા છે, તો આ તંત્રના દ્રવ્યમાન-કેન્દ્રનો$ x-$યામ શોધો. દરેક પુસ્તકનું દળ$ m$ છે.View Solution
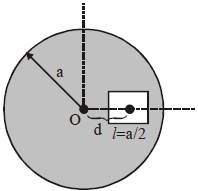
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે એક $a$ ત્રિજ્યાની વર્તુળાકાર તકતીના કેન્દ્ર $O$ થી $d=\frac{a}{2}$ અંતરે $l =\frac{ a }{2}$ લંબાઇનો એક ચોરસ ભાગ કાપીને અલગ કરેલ છે.જો બાકી રહેલા ભાગનું દ્રવ્યમાન કેન્દ્ર $O$ બિંદુથી $-\frac{a}{X},$ અંતરે હોય તો $X$(નજીકતમ પૂર્ણાંક) નું મૂલ્ય કેટલું હશે?View Solution
- 3પદાર્થ સમક્ષિતિજ સપાટી પર ગબડે છે.જો કુલઊર્જા નો $40\%$ ભાગ ચાકગતિઊર્જા હોય,તો તે પદાર્થView Solution
- 4$D$ વ્યાસ અને $L$ લંબાઈના નળાકારની લંબાઈને લંબ અને તેના ગુરૂત્વકેન્દ્રમાંથી પસાર થતી અક્ષ પર જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
- 5સમાન જડત્વની ચાકમાત્રા ધરાવતી બે તકતીઓ ની કોણીય ઝડપ ${\omega _1}\;$અને$\;{\omega _2}$છે,આ બંને તકતીઓની અક્ષ એક કરી દેવામાં આવે,તો ઊર્જાનો વ્યયView Solution
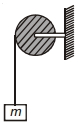
- 6આકૃતિમાં દર્શાવ્યા પ્રમાણે $m$ દળ અને $r$ ત્રિજ્યા વાળી એક તક્તી તેના કેન્દ્રને અનુલક્ષીને મુક્તપણે ભ્રમણ કરે છે. તેના ધાર પર એક દોરી વિંટાળવામાં આવે છે અને $m$ દળનો એક બ્લોક દોરીના મુક્ત છેડે જોડવામાં આવે છે. તંત્ર ને સ્થિરમાંથી મુક્ત કરવામાં આવે છે. જ્યારે બ્લોક $h$ ઊંચાઈથી નીચે તરફ ગતિ કરે છે ત્યારે બ્લોકની ઝડપ શોધો.View Solution
- 7$1\ m$ લંબાઈના હલકાં સળિયાના છેડે $ 5\ kg $ દળના બે ગોળા $ A$ અને $B $ જોડેલા છે. આ દળને બિંદુવત ધારો $A $ માંથી પસાર થતી અને મધ્યબિંદુમાંથી પસાર થતી સળિયાની લંબાઈને લંબ અક્ષો પર જડત્વની ચાકમાત્રાનો ગુણોત્તર ...... થશે.View Solution
- 8View Solutionકણ નિયમિત વર્તૂળાકાર ગતિ કરે છે. વર્તૂળના સમતલના કયાં બિંદુએ કણનું કોણીય વેગમાનનું સંરક્ષણ થશે ?
- 9View Solutionપાતળી પોલો નળાકાર બંનેને છેડેથી ખુલ્લો છે. તે રોલિંગ કર્યા વિના સરકે છે અને પછી સરક્યા વિના તેટલી જ ઝડપથી રોલિંગ કરે છે બંને કિસ્સામાં ગતિ ઊર્જાનો ગુણોત્તર ........ થશે.
- 10$L$ લંબાઇનો સળિયા બે માણસના ખંભા પર છે. છેડા પરના એક માણસ પર $ 1\over 4 $ માં ભાગનું વજનબળ લાગે છે. તો બીજો માણસ આ છેડાથી કેટલે દૂર હશે?View Solution
