\({{C}_{x}}{{H}_{y}}\,+\,\,\left( x\,\,+\,\,\frac{y}{4} \right)\,{{O}_{2}}\,\to \,xC{{O}_{2}}_{(g)}\,+\,\,\frac{y}{2}{{H}_{2}}{{O}_{(\ell )}}\)
\({{H}_{2}}O\,\) ના મોલ \(=\,\,\frac{\text{0}\text{.72}}{\text{18}}\,\,=\,\,0.04;\,\,\,\,C{{O}_{2}}\,\) ના મોલ \(=\,\,\frac{\text{3}\text{.08}}{\text{44}}\,\,=\,\,0.07\)
\(\begin{align}
\because \,\,\,x\,\,:\,\,\frac{y}{2}\,\,=\,\,0.07\,\,:\,\,0.04 \\
\Rightarrow \,\,x\,\,:\,\,y\,\,=\,\,0.07\,\,:\,\,0.08\,\,\,\Rightarrow \,\,7\,\,:\,\,8 \\
\end{align}\)
\(\because \,\,C\) અને \(\text{H}\,\,\) વચ્ચેનો ગુનોતર \(\text{x}\,\,\text{:}\,\,\text{y}\) છે
\(\therefore \,\,\text{C}\,\,\text{:}\,\,\text{H}\,\,=\,\,\text{7}\,\,\text{:}\,\,\text{8}\)
તેથી હાઈડ્રો કાર્બન નું પ્રમાણ સૂત્ર \({{\text{C}}_{\text{7}}}{{\text{H}}_{\text{8}}}\) થાય છે
Download our appand get started for free
Similar Questions
- 1View Solution......... બંધ સૌથી વધુ એસિડિક છે.
- 2પદાર્થનું અણુસૂત્ર છે તો $X$ પદાર્થની સંખ્યા કેટલી થાય ?View Solution
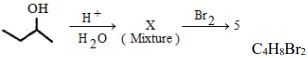
- 3નીચેની શૃંખલામાં $Z$ શું હશે?View Solution
$C{H_2} = C{H_2}\xrightarrow{{HBr}}X\xrightarrow{{{\text{Hydrolysis}}}}Y\mathop {\xrightarrow{{N{a_2}C{O_3}}}}\limits_{{I_2}{\text{ excess}}} Z$
- 4$1$-બ્યુટેનોલના હાઈડ્રેશનમાં સાંદ્ર $H_2SO_4$ સાથે ગરમ કરવાથી કઈ મુખ્ય નીપજ મળે છે ?View Solution
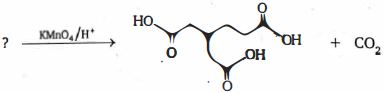
- 5View Solutionનીચે આપેલી ઓક્સિડેશન માટે કયું સંયોજન એ પ્રારંભિક સામગ્રી હતી?
- 6નીચે આપેલ પ્રક્રિયામાં બનતી મુખ્ય નીપજ '$P$' શોધો.View Solution

- 7$1,3$-બ્યુટાઇનની બ્રોમિન સાથેની યોગશીલ પ્રક્રિયા દ્વારા ........ મળે છે.View Solution
- 8$B_2D_6$ ના ઉપયોગ થી $1$- મિથાઈલસાયકલોપેન્ટેન નું હાયડ્રોબોરેશન ,અલ્કલાઈન હાઇડ્રોજન પેરોક્સાઈડ સાથે પ્રકિયા કરીને શું આપે છે ?View Solution
- 9$n - Butane \xrightarrow{{C{l_2}/hv}}$View Solution
મોનોક્લોરો ઉત્પાદનોની કુલ સંખ્યા આપો (અવકાશીય સમઘટકતા સહિત), જે ઉપરોક્ત પ્રતિક્રિયામાં કેટલા શક્ય છે.
- 10View Solutionઉપરોક્ત પ્રકિયા માં છેલી નીપજ કઈ મળશે ?

