$1 \,kg$ દળ અને $0.1 \,m$ ત્રિજ્યા ધરાવતી એક તક્તી $20 \,rad / s$ ના કોણીય વેગ સાથે ભ્રમણ કરે છે. જો દળ $0.5 \,kg$ દળને તક્તીના પરિઘ પર મૂકવામાં આવે, તો કોણીય વેગ ($rad / s$ માં) શું થાય?
Diffcult
a
(a)
(a)
Initial angular velocity is \(\omega_1=20\,rad / s\)
Moment of Inertia of disc is \(I _1= mr ^2 / 2=\frac{1 \times 0.01}{2}\,kgm ^2=0.005\,kgm ^2\)
The new moment of inertia when a particle is placed on the circumference i.e at a distance \(r\) from the axis is \(I _2= I _1+ Mr ^2=0.005+0.5\,kg \times(0.1)^2=0.01\,kgm ^2\) In this process the the angular momentum, \(J = I \omega\) will remain conserved so \(I _1 \omega_1= I _2 \omega_2\)
so the new angular velocity, \(\omega_2=\frac{ I _1}{ I _2} \omega_1=\frac{0.005}{0.01} 20=10\, rad / s\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક પાતળા સળિયાને તેના કેન્દ્રમાંથી પસાર થતી અને સળિયાને લંબ તેવી અક્ષને અનુલક્ષીને જડત્વની ચાક્માત્ર $2400 \mathrm{~g} \mathrm{~cm}^2$ છે. સળિયાની લંબાઈ લગભગ. . . . . થશે. સળિયાનું દળ $400 \mathrm{~g}$ છે.View Solution
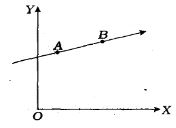
- 2$m$ દળનો એક કણ $XY$ સમતલમાં $AB$ સીધા માર્ગે $v$ વેગથી ગતિ કરે છે. સંદર્ભબિંદુ $O$ ને અનુલક્ષીને $A$ બિંદુએ કણનું કોણીય વેગમાન $L_A $ અને $B$ બિંદુએ $L_B$ હોય, તો ........View Solution
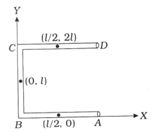
- 3$U$ આકાર ધરાવતા નિયમિત તારની બાજુનીઓની લંબાઈ $ l, 2l $ અને $ l$ છે. આકૃતિમાં દરેક તારના દ્રવ્યમાન-કેન્દ્રના યામ દર્શાવેલ છે. આ તંત્ર માટે દ્રવ્યમાન-કેન્દ્રના યામ ........View Solution
- 4એક ગરમ નક્કર ગોળો $\omega_0$ કોણીય વેગ સાથે તેના વ્યાસને અનુલક્ષીને ભ્રમણ કરી રહ્યો છે. જો તે એવી રીતે ઠંડો થાય કે તેની ત્રિજ્યાએ તેના મૂળ મૂલ્ય $\frac{1}{\eta}$ જેટલી ઘટે છે તો તેનો કોણીય વેગ થું થશે ?View Solution
- 5$M$ દળ ધરાવતા અને $R$ ત્રિજયા ધરાવતા ઘન ગોળામાંથી મહત્તમ કદ ધરાવતો એક સમઘન કાપવામાં આવે છે,તેના કેન્દ્રમાંથી પસાર થતી અને તેની કોઇ એક બાજુને લંબ એવી અક્ષને અનુલક્ષીને ચાકમાત્રા ________ થશે.View Solution
- 6View Solutionકણ વર્તૂળાકાય પથ પર ઘટતી ઝડપથી ગતિ કરે છે તો સાચું વિધાન નક્કી કરો.
- 7જ્યારે એક ઓટોમોબાઇલ $1800$ પરિભમણ પ્રતિ મિનિટ થી ભ્રમણ કરતું હોય ત્યારે તે $100\ kW$ નો પાવર ઉત્પન્ન કરે છે તો તેમાં કેટલું ટોર્ક ($N-m$ માં) લાગતું હશે?View Solution
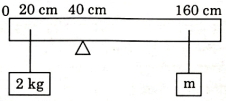
- 8$200\, cm$ લંબાઈ અને $500\, g$ દળ ધરાવતા એકસમાન સળિયાને $40\, cm$ નિશાન આગળથી ફાચર $(wedge)$ પર સંતુલિત કરવામાં આવેલ છે. $2\, kg$ ના દળને સળિયાથી $20\, cm$ અંતરે અને બીજા અજ્ઞાત દળ $m$ ને સળિયાથી $160\, cm$ નિશાની આગળથી લટકાવવામાં આવેલ છે, આકૃત્તિ જુઓ. $m$ નું એવું મૂલ્ય શોધો કે જેથી સળિયો સંતુલન સ્થિતિમાં રહે. $\left({g}=10\; m/{s}^{2}\right)$View Solution
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે એક દળરહિત $'a'$ બાજુવાળો સમબાજુ ત્રિકોણ $EFG$ ના શિરોબિંદુ પર ત્રણ $m$ દળના કણ મૂકેલા છે. ત્રિકોણ $EFG$ ના સમતલને અને બાજુ $EG$ ને લંબ બાજુ $EX$ રેખાને અનુલક્ષીને જડત્વની ચાકમાત્રા $\frac{ N }{20}\, ma ^{2}$ મળે છે. જ્યાં $N$ પૂર્ણાંક સંખ્યા છે. તો $N$ નું મૂલ્ય કેટલું હશે?View Solution
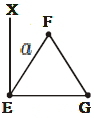
- 10$M$ દળ અને $L$ લંબાઈ ધરાવતો સળિયો ઘર્ષણરહિત સપાટી પર પડેલો છે. સપાટીને સમાંતર એક $m$ દળનો કણ $u$ વેગથી ગતિ આકરીને સળિયાને લંબ એક છેડા સાથે અથડાય છે. સંઘાત સંપૂર્ણ સ્થિતિસ્થાપક છે. અથડામણ પછી કણ સ્થિર થાય છે. દળોનો ગુણોત્તર $\left(\frac{m}{M}\right)=\frac{1}{x}$ છે. $x$ નું મૂલ્ય કેટલું હશે?View Solution
