Let the speed of bob at lowest position be \(v _{1}\) and at the highest position be \(v _{2}\).
Maximum tension is at lowest position and minimum tension is at the highest position. Now, using, conservation of mechanical energy,
\(\frac{1}{2} mv _{1}^{2}=\frac{1}{2} mv _{2}^{2}+ mg 2 l\)
\(\Rightarrow v _{1}^{2}= v _{2}^{2}+4 g l\) \(......(1)\)
Now \(T _{\max }- mg =\frac{ mv _{1}^{2}}{l}\)
\(\Rightarrow T _{\max }= mg +\frac{ mv _{1}^{2}}{l}\)
and \(T _{\min }+ mg =\frac{ mv _{2}^{2}}{l}\)
\(\Rightarrow T _{\min }=\frac{ mv _{2}^{2}}{l}- mg\)
\(\frac{ T _{\max }}{ T _{\min }}=\frac{5}{1}\)
\(\Rightarrow \frac{ mg +\frac{ mv _{1}^{2}}{l}}{\frac{ mv _{2}^{2}}{l}- mg }=\frac{5}{1}\)
\(\Rightarrow mg +\frac{ mv _{1}^{2}}{l}=\left[\frac{ mv _{2}^{2}}{l}- mg \right] 5\)
\(\Rightarrow mg +\frac{ m }{l}\left[ v _{2}^{2}+4 g l\right]=\frac{5 mv _{2}^{2}}{l}-5 mg\)
\(\Rightarrow mg +\frac{ mv _{2}^{2}}{l}+4 mg =\frac{5 mv _{2}^{2}}{l}-5 mg\)
\(\Rightarrow 10 mg =\frac{4 mv _{2}^{2}}{l}\)
\(v _{2}{ }^{2}=\frac{10 \times 10 \times 1}{4}\)
\(\Rightarrow v _{2}^{2}=25 \Rightarrow v _{2}=5 m / s\)
Thus, velocity of bob at highest position is \(5 m / s\)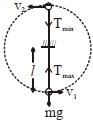
Download our appand get started for free
Similar Questions
- 1માનવનું હૃદય $10cm$ દબાણની વિરૂદ્ધમાં ધમનીઓ મારફતે $75 cc$ જેટલું રૂધિર એક ધબકારે ડિસ્ચાર્જ કરે છે. જો પ્રતિ મિનિટ $72 $ ધબકારા થતા હોય તો હૃદયનું કાર્યમ......$W$ વોટમાં ગણો. ( ઘનતા $= 13.6 g/cc $ અને $g = 9.8 m/s^2).$View Solution
- 2એક $10 g$ ની ગોળીને $800 m/s$ વેગ સાથે છોડવામાં આવે છે. $1m$ જાડાઈની કાદવની દિવાલમાંથી પસાર થયા પછી તેનો વેગ ઘટીને $100 m/s$ થાય છે. કાદવની દિવાલ વડે આપવામાં આવતો સરેરાશ અવરોધ.....$N$ શોધો.View Solution
- 3એક અચળ $F$ ની અસર હેઠળ સ્થિર અવસ્થાથી શરૂ કરી $m$ દળે એક નિયત અંતર $d$ કાપવા દરમિયાન શરૂ થઈને $l$ જેટલું નિશ્ચિત અંતર કાપવા દરમિયાન $m$ દળે મેળવેલી ગતિ ઉર્જાView Solution
- 4$10 \;g$ દળની ગોળી રાઇફલમાંથી $1000 \;m/s$ ના પ્રારંભિક વેગથી બહાર નીકળે છે અને સમાન સ્તરે $500\; m/s$ ના વેગથી પૃથ્વી સાથે અથડાય છે. હવાના ઘર્ષણ વિરુદ્વ કરવું પડતું કાર્ય (જૂલમાં) કેટલું હશે?View Solution
- 5$1\,kg$ દળ ધરાવતો એક પદાર્થ $3\,kg$ દળના સ્થિર પદાર્થ સાથે સ્થિતિસ્થાપક સન્મુખ સંઘાત ઉત્પન્ન કરે છે. સંધાત બાદ નાનો પદાર્થની ગતિની દિશા ઉલટાઈ જાય છે અને તે $2\,m / s$ ની ઝડપથી ગતિ કરે છે. તો સંધાત પહેલાની નાના દળવાળા પદાર્થની ઝડપ $.........ms ^{-1}$ હશે.View Solution
- 6એક ઓલમ્પિક રમતમાં એથ્લીટ્સ $100$ $m$ અંતર $10$ $s$ માં કાપે છે, તો તેની અંદાજિત ગતિઊર્જાનો ગાળો કેટલો હશે?View Solution
- 7કણની સ્થિતિઊર્જા $U = A - B{x^2} $ છે.તો કણ પર લાગતું બળView Solution
- 8$5\; kg$ દળના પદાર્થનું વેગમાન $10\; kg-m/s$ છે.તેના પર $0.2\; N $ બળ $ 10 \;seconds $ સમય સુધી લાગતાં ગતિઊર્જામાં થતો વધારો.....$J$View Solution
- 9$100 m $ લંબાઇ અને $1 m$ ઉંચાઇ ધરાવતા ઢાળ પર $30,000 kg$ નો ટ્રક $30 km/hr$ ની ઝડપથી ગતિ કરે,તો ટ્રકનો પાવર કેટલા .......... $kW$ થશે? $( g = 10m{s^{ - 1}}) $View Solution
- 10એક $5\,kg$ દળવાળા બ્લોકને વિરામ શરૂ કરીને ખેંચવામાં આવે છે ત્યારે તેની સુંવાળી ત્રાંસી સપાટી $30^{\circ}$ નો ખૂણો ક્ષિતિજ સાથે બનાવે છે. લાગુ પડતો પ્રવેગ $1\,ms ^{-2}$ છે. $t =10\,s$ ના સમયે આરામથી તેના ખેંચાણ બળને કારણે અપાતો પાવર $........\,W$ છે. [$g =10\,ms ^{-2}$ ઉપયોગ કરો] (નજીકની પૂર્ણાક કિંમત શોધો)View Solution
