$1 \mathrm{~m}$ લંબાઈનું સાદું લોલક $1 \mathrm{~kg}$ દળનું દોલક ધરાવે છે. તેના પર $10^{-2} \mathrm{~kg}$ દળની બુલેટ $2 \times 10^2 \mathrm{~ms}^{-1}$ ઝડપથી અથડાય છે. આ બુલેટ દોલકની અંદર ખૂંચી જાય છે. દોલકે પાછુ વળે તે પહેલાની ઉંચાઈ_______છે. ( $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$લો)
JEE MAIN 2024, Diffcult
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
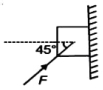
- 1$4 \,kg$ દળ નાં એક બ્લોકને આકૃતિમાં દર્શાવ્યા મુજબ લીસી શિરોલંબ દિવાલની સામે બળ $F$ લગાડીને સ્થિર મુકેલો છે. તો લગાડવામાં આવતું બળ .......... $N$ છે? $\left(g=10 \,m / s ^2\right)$View Solution
- 2View Solutionજો તંત્ર પર લાગતું પરિણામી (Net) બળ શૂન્ય હોય તો
- 3એક $m$ દળના નાના દડાને જમીન પરથી ઉપર તરફ $u$ વેગથી ફેકવામાં આવે છે. દડો $mkv ^{2}$ જેટલું અવરોધક બળ અનુભવે છે. જ્યાં $v$ તેની ઝડપ છે. તો દડાએ પ્રાપ્ત કરેલી મહતમ ઊંચાઈ કેટલી હશે?View Solution
- 4$0.3\,kg\,m/s$ રેખીય વેગમાન ધરાવતા રેખીય ગતિ કરતાં $5\,g$ દળના પદાર્થે $5\,s$ માં કાપેલ અંતર $..........\,m$ હશે.View Solution
- 5$0.3 kg$ ના પદાર્થ પર લાગતું બળ $F = - kx$ ,$k = 15\,N/m.$ છે.તો ઉદ્ગમબિંદુથી $20\, cm$ અંતરે પદાર્થને મૂકવામાં આવે,ત્યારે તેનો પ્રવેગ .......... $m/s^2$ હશે.View Solution
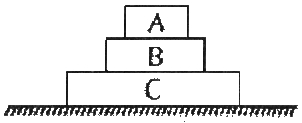
- 6આકૃતિમાં દર્શાવ્યા પ્રમાણે ત્રણ બ્લોક્સને મુકેલાં છે. $A, B$ અને $C$ નો દળ અનુક્રમે $m_1, m_2$ અને $m_3$ છે. બ્લોક $'B'$ પર બ્લોક ' $C$ ' વડે સગાડવામાં આવેલું બળ ..... છે.View Solution
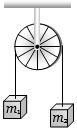
- 7$m_1=5\,kg$ અને $m_2=4.8 \,kg$ ના બે પદાર્થોને એક હલકી દોરી વડે ઘર્ષણ રહિત ગરગડી પરથી આકૃતિમાં દર્શાવ્યા મુજબ લટકાવેલ છે.જયારે બંને પદાર્થોને ગતિ કરવા મુકત કરવામાં આવે ત્યારે આ પદાર્થોમાં .......... $m/s^{2}$ પ્રવેગ ઉત્પન્ન થાય.View Solution
- 8View Solutionએક વ્યક્તિ લિફટમાં ઉભેલો છે. તે કઈ પરિસ્થિતિમાં વજનરહિત સ્થિતિ અનુભવશે ?
- 9ત્રણ બળો $\vec{F}_1=(2 \hat{i}+4 \hat{j}) \,N ; \vec{F}_2=(2 \hat{j}-\hat{k}) \,N$ અને $\vec{F}_3=(\hat{k}-4 \hat{i}-2 \hat{j}) \,N$ ને ઊગમબિંદુ પર સ્થિર રહેલાં $1 \,kg$ દળનાં પદાર્થ પર લગાડવામાં આવે છે. તો સમય $t=2 \,s$ પદી પદાર્થનું સ્થાન ક્યાં હશે.View Solution
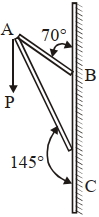
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે બે દળરહિત સળિયા $AB$ અને $AC$ દ્વારા એક ફ્રેમ બનાવેલ છે. $A$ બિંદુ પર $\overrightarrow{ P }$ બળ લાગે છે જેનું મૂલ્ય $100\; N$ છે. તો બળ $\overrightarrow{ P }$ નો $AC$ ની દિશામાંનો ઘટક $x\;N$ હોય તો $x$નું મૂલ્ય નજીકના પૂર્ણાંકમાં કેટલું હશે?View Solution
[$\sin \left(35^{\circ}\right)=0.573, \cos \left(35^{\circ}\right)=0.819$ $\left.\sin \left(110^{\circ}\right)=0.939, \cos \left(110^{\circ}\right)=-0.342\right]$
