\(\overrightarrow{\mathrm{F}}=\left(6 \mathrm{t} \hat{\mathrm{i}}+6 \mathrm{t}^2 \hat{\mathrm{j}}\right) \mathrm{N}\)
\(\overrightarrow{\mathrm{F}}=\mathrm{ma}=\left(6 \mathrm{t}+6 \mathrm{t}^2 \hat{\mathrm{j}}\right)\)
\(\overrightarrow{\mathrm{a}}=\frac{\overrightarrow{\mathrm{F}}}{\mathrm{m}}=\left(3 \mathrm{t}+3 \mathrm{t}^2 \hat{\mathrm{j}}\right)\)
\(\overrightarrow{\mathrm{v}}=\int_0^{\mathrm{t}} \overrightarrow{\mathrm{a}} d \mathrm{~d}=\frac{3 \mathrm{t}^2}{2} \hat{\mathrm{i}}+\mathrm{t}^3 \hat{\mathrm{j}}\)
\(\mathrm{P}=\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{v}}=\left(9 \mathrm{t}^3+6 \mathrm{t}^5\right) \mathrm{W}\)
Download our appand get started for free
Similar Questions
- 1$2kg$ ના પદાર્થને $490 J$ ગતિઊર્જાથી ઉપર ફેંકવામાં આવે છે.તો ................. $\mathrm{m}$ ઊંચાઇએ ગતિઊર્જા અડધી થાય?View Solution
- 2એક ગનમાંથી એક બુલેટ ખૂબ જ મોટા લાકડાના બ્લોકમાં મારતાં ગોળી બ્લોકમાં $6 m$ ગતિ કરે ત્યારે તેનો વેગ અડધો થાય છે, તો તે વધારાનું ............. $\mathrm{cm}$ અંતર કાપી સ્થિર થશે.View Solution
- 3નીચે બે વિધાનો આપેલા છે. એક ને કથન $A$ અને બીજાને કારણ $R$ દ્વારા દર્શાવવામાં આવ્યા છે.View Solution
કથન $A$ : $M$ દળ ધરાવતો તેમજ $'u'$ ઝડપથી ગતિ કરતો પદાર્થ $'P'$ પ્રારંભમાં વિરામ સ્થિતીમાં છે અને $‘m'$ દળ ધરાવતાં $‘Q$ પદાર્થ સાથે તે સીધો સ્થિતિસ્થાપક સંઘાત કરે છે. જો $m<< M$ હોય તો પદાર્થ $‘Q'$ ની સંઘાત પછી મહત્તમ ઝડપ $‘2u’$ હોય છે.
કારણ $R$ : સ્થિતિસ્થાપક સંધાત દરમ્યાન વેગમાન અને ગતિઊર્જા બંનેનું સંરક્ષણ થાય છે.
ઉપરોક્ત જણાવેલ કથન અને કારણને અનુલક્ષીને નીચે આપેલ વિકલ્પોમાંથી સૌથી યોગ્ય જવાબ પસંદ કરો
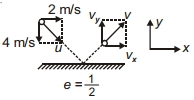
- 4$u$ ઝડપે લીસી અને સમક્ષિતિજ સપાટી સાથે ત્રાંસી અથડામણ અનુભવે છે. જેના $x$ અને $y$ ઘટકો દર્શાવેલ છે. જો રેસ્ટિટ્યુશન ગુણાંક $\frac{1}{2}$ હોય, તો અથડામણ પછીના $x$ અને $y$ ના ઘટકો $v_x$ અને $v_y$ અનુક્રમે ...... હશે ?View Solution
- 5$0.01\; kg$ દળના પદાર્થનો વેગ $4\hat i + 16\hat k\; ms^{-1}$ થી $8\hat i + 20\hat j\,m{s^{ - 1}}$ થાય,તો થતું કાર્ય....$J$View Solution
- 6$100 gm $ અને $250 gm$ દળના બે દડાઓ $A$ અને $B$ અવગણ્યદળ વાળી તાણેલી (ખેંચેલી) સ્પ્રિંગ વડે જોડેલા છે અને જે લીસા ટેબલ પર મૂકેલા છે. જ્યારે બંને દડાઓને એક સાથે છોડવામાં આવે જેમાં $B$ દડાનો પ્રારંભિક પ્રવેગ $10 cm/sec^2$ પશ્ચિમ દિશામાં લાગે છે. $A $ દડા ના પ્રારંભિક પ્રવેગનું મૂલ્ય અને દિશા શોધો.View Solution
- 7$1 kg $ દળના એક બોકસને $1m$ લંબાઈના સમક્ષિતિજ સમતલ પર લટકાવેલ છે, જેમાં $8 N$ બળને લીધે શિરોલંબ દિશામાં તેની ઉંચાઈમાં $2m$ નો વધારો થાય છે. તો થતું ચોખ્ખુ કાર્ય કેટલા .....જૂલ હશે ?View Solution
- 8પદાર્થને ઉપર તરફ ફેંકતાં તેની મહત્તમ ઊંચાઇ $h$ છે.તો$\frac{{3h}}{4},$ઊંચાઇએ ગતિઊર્જા અને સ્થિતિઊર્જાનો ગુણોત્તરView Solution
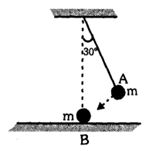
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે લોલક $A$ ને શિરોલંબથી $30°$ ના ખૂણેથી મુક્ત કરતાં સમાન દળના લોલક $B $ ને અથડાય છે. અથડામણ બાદ લોલક $A $ કેટલા .....$m$ ઉંચાઈએ પહોંચશે ? લોલકનું કદ અવગણો અને અથડામણ સ્થિતિ સ્થાપક ધારો.View Solution
- 10સ્થિર સ્થિતિમાં રહેલો એક કણ એ $x$ અને $y$ દળનાં બે કણોમાં વિસ્ફોટ પામે છે. જેઓ એકબીજાથી વિરુદ્ધ દિશામાં $v_1$ અને $v_2$ વેગ સાથે ગતિ કરે છે. તેમની ગતિઉર્જાઓ $\left(E_1: E_2\right)$ નો ગુણોત્તર છેView Solution
