$2\, kg$ નો બ્લોક $3.0 \,m/s$ ના સમક્ષિતિજ વેગથી ગતિ કરે છે.જેના પર $ 4\, sec$ સુધી $4 \,N$ નું લંબબળ લગાડતા બ્લોક ........... $m$ અંતર કાપશે.
Medium
b
(b) Displacement of body in \(4 \,sec\) along \(OE\)
(b) Displacement of body in \(4 \,sec\) along \(OE\)
\({s_x} = {v_x}t = 3 \times 4 = 12\;m\)
Force along \(OF\) (perpendicular to \(OE\)) \(= 4\, N\)
\(\therefore {a_y} = \frac{F}{m} = \frac{4}{2} = 2\;m/{s^2}\)
Displacement of body in \(4\, sec\) along \(OF\)
\(⇒\) \({s_y} = {u_y}t + \frac{1}{2}{a_y}{t^2}\)\( = \frac{1}{2} \times 2 \times {(4)^2} = 16\;m\) [As \({u_y} = 0\)]
\(\therefore \) Net displacement \(s = \sqrt {s_x^2 + s_y^2} \; = \sqrt {{{(12)}^2} + {{(16)}^2}} = 20\;m\)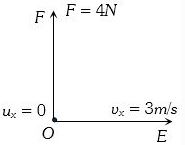
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
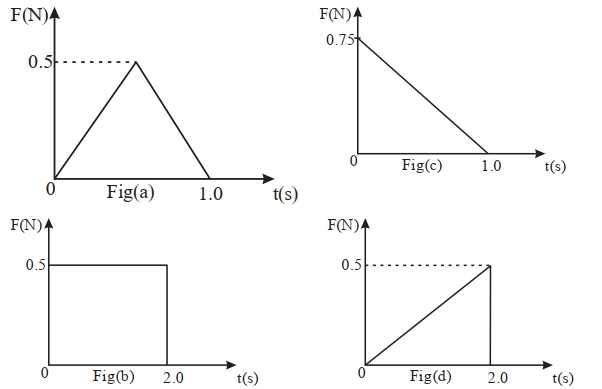
- 1આકૃતિઓ $(a), (b), (c)$ અને $(d)$ એ બળનો સમય સાથેનો ફેરફાર દર્શાવે છે.View Solution
$..........$ આકૃતિમાં સૌથી વધારે આધાત હશે.
- 2$5 \,m$ ઊંચાઇ પરથી $400 \,gm$ ના દડાને મુકત કરવામાં આવે છે.તે જમીન પર આવતા $100\, N$ નું બળ ઉપર તરફ લગાવતાં $20 \,m$ ઊંચાઇએ જાય છે.તો બોલ અને બેટ વચ્ચેનો સંપર્ક સમય ........... $\sec$ હશે. $[g = 10\,m/{s^2}]$View Solution
- 3જો $M_2 = 2M_1 $ અને $\theta = 30^o$ હોય, તો $ M_2$ નો પ્રવેગ $ a $ છે. જો બ્લોકના સ્થાન ઉલટાવવામાં આવે,તો $M_2$ નો પ્રવેગ કેટલો થાય?View Solution
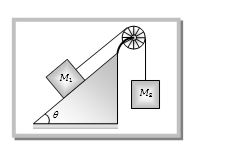
- 4જો $ M_1 = M_2 = 5\, kg $ અને $\theta = {30^o}$ હોય,તો દોરીમાં તણાવ ........... $N$ થશે.View Solution

- 5એક ફટાકડાનું રોકેટ $400 \,m / s$.નાં વેગ સાથે $0.05 \,kg / s$ ની દરે વાયુઓ મુક્ત કરે છે. તો રોકેટ પરલાગતું પ્રવેગિત બળ છેView Solution
- 6View Solutionવિધાન: વાહનમાં રહેલો ચાલક સીધા રોડ પર અચળ ઝડપથી ગતિ કરતો હોય તે જડત્વની નિર્દેશફ્રેમ છે.
કારણ: જે નિર્દેશફ્રેમમાં ન્યુટનના ગતિના નિયમો લાગુ પાડી શકાતા હોય તે અજડત્વની નિર્દેશફ્રેમ છે.
- 7$6000\, kg$ ની લિફ્ટને ઉપર તરફ $5 m/sec^2$ ના પ્રવેગથી ગતિ કરાવતા,લિફ્ટના કેબલમાં ........... $N$ તણાવ ઉત્પન્ન થશે.View Solution
- 8${m_1},\,{m_2}$ અને ${m_3}$ દળના બ્લોકને વજનરહિત દોરી વડે બાંઘીને ઘર્ષણરહિત સપાટી પર મૂકેલાં છે. $m_3$ દળ પર $T$ બળ લગાડવામાં આવે,તો ${m_2}$ અને ${m_3}$ વચ્ચેની દોરીમાં તણાવ કેટલો થશે?View Solution
- 9View Solutionજો તંત્ર પર લાગતું પરિણામી (Net) બળ શૂન્ય હોય તો
- 10એક ન્યુટ્રોનનું દળ $1.67 × 10^{-27} kg $ છે અને તે $ 10^8m/s$ ના વેગથી ગતિ કરતી વખતે સ્થિર સ્થિતિમાં રહેલા એક ડ્યુટેરોન સાથે અથડાય છે અને તેની સાથે ચોટી જાય છે. જો ડ્યુટેરોનનું દળ $3.34 ×10^{-27 } kg$ હોય તો બંનેના જોડાણની ઝડપ કેટલી હશે?View Solution
