$20\,ms ^{-1}$ ના વેગ સાથે એક કાર $P$ કે જેના હોર્ન દ્વારા ઉત્પન્ન થતા ધ્વનિની આવૃત્તિ $400\,Hz$ છે. તે જ દિશામાં એક બીજી કાર $Q$ પ્રથમ કારની પાછળ $40\,ms ^{-1}$ ના વેગ સાથે ગતિ કરે છે. કારના મુસાફર દ્વારા સંભળાતી આવૃત્તિ અંદાજિત આવૃત્તિ ........ $Hz$ છે. [ધ્વનિનો વેગ $=360\,ms ^{-1}$, લો]
JEE MAIN 2023, Medium
Download our app for free and get started
b
\(f=f_0\left(\frac{c+v_0}{c+v_s}\right)\)
\(f=f_0\left(\frac{c+v_0}{c+v_s}\right)\)
\(f=400\left(\frac{360+40}{360+20}\right)\)
\(f=421\,Hz\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$256\, Hz$ નો સ્વરકાંટો $25.4\, cm$ લંબાઈ ધરાવતી ક્લોઝ્ડ પાઇપની સાથે અનુનાદ કરે છે.જો પાઈપની લંબાઈ $2\, mm$ જેટલી વધારવામાં આવે તો પ્રતિ સેકન્ડે કેટલા સ્પંદ સંભળાશે?View Solution
- 2$100 \,Hz$ આવૃત્તિ વાળું તરંગ દોરી પર દઢ છેડા તરફ જાય છે. જ્યારે આ તરંગ પરાવર્તન પામીને પાછું આવે ત્યારે દઢ છેડાથી $10\,cm$ અંતરે નિસ્પંદ બિંદુ બને છે. આપત (અને પરાવર્તિત) તરંગની ઝડપ ($m/s$ માં) કેટલી થાય?View Solution
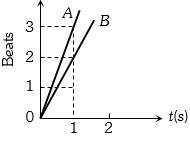
- 3સ્વરકાંટા $P$ અને $Q$ ને સાથે કંપન કરાવતા ઉત્પન્ન થતાં સ્પંદ $OA$ રેખા દ્વારા દર્શાવવામાં આવે છે, $Q$ પર મીણ લગાવાથી ઉત્પન્ન થતાં સ્પંદ $OB$ રેખા દ્વારા દર્શાવવામાં આવે છે,જો $P$ ની આવૃત્તિ $341 Hz$ હોય,તો $Q$ ની આવૃત્તિ કેટલી ... $ Hz$ થાય?View Solution
- 4અનુનાદિત નળી પ્રથમ વાર $16cm$ અને બીજી વાર $49cm$ એ સ્વરકાંટા સાયે અનુનાદિત થાય છે.તો સ્વરકાંટાની આવૃત્તિ કેટલી થાય? (હવામાં ધ્વનિનો વેગ $330 m/s$ છે.)View Solution
- 5$7.0 \times 10^{-3}\,kg\,m ^{-1}$ દળ પ્રતિ લંબાઈ દીઠ સ્ટીલનો તાર $70\,N$ ના તણાવ હેઠળ છે. તારમાં લંબગત તરંગોની ઝડપ $.........m/s$ હશે.View Solution
- 6$9 \times 10^{-3} \,kg\, cm ^{-3}$ ઘનતા ધરાવતા તારને બે $1\, m$ દૂર રહેલા ક્લેમ્પ સાથે જડેલ છે. તારમાં પરિણામી વિકૃતિ $4.9 \times 10^{-4}$ હોય તો તારમાં લંબગત કંપનની નાનામાં નાની આવૃતિ કેટલા $HZ$ હશે? (જવાબ નજીકતમ પૂર્ણાંકમાં આપો)View Solution
(તારનો યંગ મોડ્યુલસ $Y =9 \times 10^{10}\, Nm ^{-2}$ )
- 7પર્વત તરફ ગતિ કરતો કારનો ચાલક $600 \,Hz$ આવૃતિનો હોર્ન વગાડે છે. કારની ઝડપ $30 \,m / s$ છે. અને હવામાં અવાજની ઝડપ $330 \,m / s$ હોય, તો ચાલક દ્વારા સંભળાતા પરાવર્તીત અવાજની આવૃતિ ......... $Hz$ છે.View Solution
- 8$30\; m/s$ ની ઝડપથી પહાડ તરફ ગતિ કરતી કારનો ડ્રાઇવર $600 \;Hz$ ની આવૃતિવાળો હોર્ન વગાડે છે. જો હવામાં ઘ્વનિનો વેગ $330 \;m/s$ હોય, તો ડ્રાઇવરને સંભળાતી પરાવર્તિત ધ્વનિની આવૃતિ ($Hz$ માં) કેટલી હશે?View Solution
- 9બંધ પાઇપમાં $1000 Hz$ ના તરંગો ઉત્પન્ન કરવામાં આવે,ત્યારે $6$ નિસ્પંદ બિંદુ વચ્ચેનું કુલ અંતર $85cm$ છે,તો ધ્વનિની ઝડપ કેટલી ..... $m/s$ થાય?View Solution
- 10$450 Hz$ આવૃત્તિવાળા ઉદ્ગમ સ્થિર અવલોકનકાર તરફ $33\, m/s$ વેગથી ગતિ કરતો હોય તો કેટલી આવૃત્તિ સંભળાય? (હવામાં ધ્વનિનો વેગ $332 \,m/s$ છે.)View Solution