$298\,K$ તાપમાન પર $pH =10$ના $HCl$ના દ્રાવણમાં પ્લેટિનમ તારને ડુબાડીને હાઈડ્રોજન વાયુ વિદ્યુતધ્રુવ બનાવવામાં આવે છે અને એક $atm$ દબાણ પર પ્લેટિનમની આજુબાજુ હાઇડ્રોજન વાયુ પસાર કરવામાં આવે છે. વિદ્યુતધ્રુવનો પોટેન્શિયલ ......... $V$ હશે.
AIIMS 2019, Medium
Download our app for free and get started
a
The reaction occurs at standard hydrogen electrode $(S.H.E)$ is given below :
The reaction occurs at standard hydrogen electrode $(S.H.E)$ is given below :
$H _{2} \rightarrow 2 H ^{+}+2 e ^{-}$
At $1\,atm$ pressure, $pH$ is equal to $10$ .
Therefore,
$\left[ H ^{+}\right]=10^{-10}$
The standard reduction potential of $S.H.E$ is equal to zero.
Apply Nernst equation,
$E_{ H _{2} / H ^{+}}=0-\frac{0.059}{2} \log \frac{\left(10^{-10}\right)^{2}}{1}$
$=0.0295 \times 20$
$=0.59 \,V$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$25^o$ સે.પ્રક્રિયાનો પ્રમાણિત રીડક્શન પોટેન્શિયલ નીચે મુજબ છે. કયો પ્રબળ રીડ્યુસીંગ કર્તા છે?View Solution
$Zn^{2+}(aq) + 2e^{-} $ $\rightleftharpoons$ $ Zn (s)$ , $E^o_{RP}= -0.762\, V$,
$Cr^{3+}(aq) + 3e^{-} $ $\rightleftharpoons$$ Cr(s)$, $E^o_{RP} = -0.740\, V$
$2H^{+}(aq) + 2e^{-} $$\rightleftharpoons$$ H_2(g)$, $E^o_{RP} = 0.00\,V$,
$Fe^{3+}_{(aq)} + 2e^{-} $$\rightleftharpoons$$ Fe^{2+}(aq)$ , $E^o_{RP} = 0.77 \,V$
- 2નીચે આપેલા અર્ધકોષોથી બનતા કોષનો $EMF$ કેટલા ............ $\mathrm{V}$ થશે?View Solution
$M{g^{2 + }} + 2{e^ - } \to Mg(s);\,\,E = - 2.37\,V$
$C{u^{2 + }} + 2{e^ - } \to Cu(s);\,\,\,E = + 0.33\,V$
- 3એલ્યુમિનિયમ ક્લોરાઈડના દ્રાવણ એલ્યુમિનિયમનો $1$ ગ્રામ પરમાણુ (પરમાણુ ભાર $=27$ ) પ્રાપ્ત કરવા માટે ............ $\mathrm{N}$ ઇલેક્ટ્રોનોની જરૂર પડશે. (જ્યાં, $N$ એવોગેડ્રો આંક છે)View Solution
- 4નીચેની પ્રક્રિયા માટે કોષનો $ emf$ આપેલ છે. $Zn (s) + Ni^{2+}_{(aq)}\, (a = 0.1) \rightarrow Zn^{2+}_{(aq)}\, (a = 1.0) + Ni\,\, 298\,K$. એ $0.5105\, V$ જોવા મળે છે કોષમાં પ્રમાણિત $e$ કેટલા. ................ $\mathrm{V}$ છે?View Solution
- 5$298 \mathrm{~K}$. પર કોષ (image) ના વડે તેને વધારી શકાય છે.View Solution
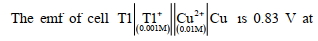
- 6$298$ $K$ પર આપેલ અર્ધ કોપ માટે પોટેન્શિયલ (-)_________ $\times 10^{-2} \mathrm{~V}$ છે.View Solution
$2 \mathrm{H}_{(\mathrm{aq})}^{+}+2 \mathrm{e}^{-} \rightarrow \mathrm{H}_2(\mathrm{~g})$
${\left[\mathrm{H}^{+}\right]=1 \mathrm{M}, \mathrm{P}_{\mathrm{H}_2}=2 \mathrm{~atm}}$
(Given: $2.303 \mathrm{RT} / \mathrm{F}=0.06 \mathrm{~V}, \log 2=0.3$ )
- 7$Zn \rightarrow Zn^{+2} + 2e^{-}$ અર્ધપ્રક્રિયા માટેના પ્રમાણિત ઑક્સિડેશન પોટૅન્શિયલનાં મૂલ્યો આ પ્રમાણે આપેલ છે : $E^{0}_{Oxi} = +0.76\,V$, $Fe \rightarrow Fe^{2+} + 2e^{-}$ , $E^{0}_{Oxi} = +0.41\,V$. $Fe^{2+} + Zn \rightarrow Zn^{2+} + Fe$ પ્રક્રિયા માટે કોષનો પોટૅન્શિયલ ............ $\mathrm{V}$ શોધો.View Solution
- 8$NaI, NaNO _{3}$ અને $AgNO _{3}$ ની સિમિત મોલર વાહકતાઓ (limiting molar conductivities) અનુક્રમે $12.7,12.0$ અને $13.3\, mS m { }^{2}\, mol ^{-1}$ છે. (બધા $25^{\circ} C$ તાપમાને). તો આ જ તાપમાને $AgI$ ની સિમિત મોલર વાહકતા $......\,mS m ^{2}\, mol ^{-1}$ છેView Solution
- 9$18$ ગ્રામ $ H_2O$ ના વિદ્યુત વિભાજ્યના વિઘટન માટે $ 3 $ એમ્પિયર પ્રવાહ કેટલા ........... કલાક સમય સુધી પસાર કરવામાં આવે છે?View Solution
- 10તત્વ $I, II, III$ અને $IV$ ના $E^{0}_{Red} $ નાં મૂલ્યો અનુક્રમે $-3.04 \,V, -1.90\, V, 0.00 \,V, 1.90\, V$ હોય, તો મહત્તમ રિડકશનકર્તા તરીકેની ક્ષમતા ધરાવતું તત્વ ..... હશે.View Solution