When alkenes are treated with \(HBr\) in the presence of peroxides, an anti-Markovnikov addition occurs in the sense that the hydrogen atom becomes attached to the carbon atom with the fewer hydrogen atoms.
The product formed has two chirality centres, therefore, four stereoisomers \(\left(2^{2}\right)\) will exist.
\(\begin{array}{*{20}{c}}
{\,\,\,\,\,C{H_3}} \\
| \\
{C{H_3} - C{H_2} - C = CH - C{H_3}}
\end{array}\) \(\xrightarrow[{Peroxide}]{{HBr}}\) \(\mathop {\begin{array}{*{20}{c}}
{\,\begin{array}{*{20}{c}}
{\,\,\,\,\,\,C{H_3}} \\
|
\end{array}} \\
{C{H_3} - C{H_2} - {}_*CH - \mathop {CH}\limits^{*\,} - C{H_3}} \\
{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,|} \\
{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,Br}
\end{array}}\limits_{Major\,\,product} \)
Download our appand get started for free
Similar Questions
- 1$\underset{(Calcium\,carbide)}{\mathop{Ca{{C}_{2}}}}\,\xrightarrow{{{H}_{2}}O}(A)\xrightarrow{\operatorname{Re}d\,\,hot\,Cu\,tube}(B),$ પ્રકિયા ની નીપજ $(B)$ શું હશે ?View Solution
- 2View Solutionઘન મિથેન એ .....
- 3$CH_3 - C \equiv C - CH_2CH_3$ $\xrightarrow[{\left( {ii} \right)\,Hydrolysis}]{{\left( i \right)\,{O_3}}}$ પ્રક્રિયાની નીપજો ..... થશે.View Solution
- 4પ્રકાશની હાજરીમાં સંયોજન $(E)$ માંથી બ્રોમીનેશન પ્રક્રિયા દરમ્યાન કયો હાઇડ્રોજન સહેલાયથી વિસ્થાપિત થશે?View Solution
$\mathop {C{H_3} - }\limits_\delta \mathop {C{H_2} - }\limits_\gamma \mathop {CH = }\limits_\beta \mathop {C{H_2}}\limits_\alpha $
$(E)$
- 5View Solutionઆ પ્રકિયા ની નીપજ શું હશે ?
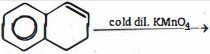
- 6View Solutionપ્રોપીન અને પ્રોપાઇન વચ્ચે ફરક તપાસવા માટે કયો રીએજન્ટ વપરાય છે?
- 7મિથેન ના ક્લોરીનેશન ના મુક્ત મુલક ના તબબ્કા માં શ્રુંખલા પસંદ કરોView Solution
$(1) \,Cl_2 \to 2Cl^\bullet $
$(2)\, Cl^\bullet + CH_4 \to CH_3Cl + H^\bullet $
$(3)\, Cl^\bullet +CH_4 \to CH^\bullet _3 + HCl$
$(4)\, H^\bullet +Cl_2 \to HCl + Cl^\bullet $
$(5)\, CH^\bullet _3 + Cl_2 \to CH_3Cl + Cl^\bullet $
- 8$130^o$ સે. એ $n-$બ્યુટીન અને બ્રોમીન વચ્ચેની પ્રક્રિયાની નીપજ કઈ છે ?View Solution
- 9View Solutionનીચે પૈકી કયું એસિડિક હાઇડ્રોજન ધરાવે છે?
- 10નીચે આપેલ પ્રક્રિયાઆની શ્રેણીમાં મુખ્ય નીપજ શું થશે $?$View Solution
$n - Bu -\equiv\frac{(i) n-BuLi,n - C _{5} H _{11} Cl}{(ii) Lindlar\,\, cat, H _{2}}$
