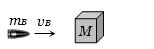
$50 g $ ની ગોળી $10 m/s $ ના વેગથી $950 gm$ ના સ્થિર બ્લોકમાં ધૂસીને સ્થિર થઇ જાય છે.તો તંત્ર કેટલા ................. $\%$ ગતિઊર્જા ગુમાવશે?
Diffcult
b
(b)Initial K.E. of system = K.E. of the bullet =\(\frac{1}{2}{m_B}v_B^2\)
By the law of conservation of linear momentum
\({m_B}{v_B} + 0 = {m_{{\rm{sys}}{\rm{.}}}} \times {v_{{\rm{sys}}{\rm{.}}}}\)
==> \({v_{{\rm{sys}}{\rm{.}}}} = \frac{{{m_B}{v_B}}}{{{m_{{\rm{sys}}{\rm{.}}}}}} = \frac{{50 \times 10}}{{50 + 950}} = 0.5\;m/s\)
Fractional loss in K.E. = \(\frac{{\frac{1}{2}{m_B}v_B^2 - \frac{1}{2}{m_{{\rm{sys}}{\rm{.}}}}v_{{\rm{sys}}{\rm{.}}}^2}}{{\frac{1}{2}{m_B}v_B^2}}\)
By substituting \({m_B} = 50 \times {10^{ - 3}}kg,\;{v_B} = 10\;m/s\)
\({m_{{\rm{sys}}{\rm{.}}}} = 1kg,\;{v_s} = 0.5\;m/s\) we get
Fractional loss = \(\frac{{95}}{{100}}\)
Percentage loss \(= 95\%\)
(b)Initial K.E. of system = K.E. of the bullet =\(\frac{1}{2}{m_B}v_B^2\)
By the law of conservation of linear momentum
\({m_B}{v_B} + 0 = {m_{{\rm{sys}}{\rm{.}}}} \times {v_{{\rm{sys}}{\rm{.}}}}\)
==> \({v_{{\rm{sys}}{\rm{.}}}} = \frac{{{m_B}{v_B}}}{{{m_{{\rm{sys}}{\rm{.}}}}}} = \frac{{50 \times 10}}{{50 + 950}} = 0.5\;m/s\)
Fractional loss in K.E. = \(\frac{{\frac{1}{2}{m_B}v_B^2 - \frac{1}{2}{m_{{\rm{sys}}{\rm{.}}}}v_{{\rm{sys}}{\rm{.}}}^2}}{{\frac{1}{2}{m_B}v_B^2}}\)
By substituting \({m_B} = 50 \times {10^{ - 3}}kg,\;{v_B} = 10\;m/s\)
\({m_{{\rm{sys}}{\rm{.}}}} = 1kg,\;{v_s} = 0.5\;m/s\) we get
Fractional loss = \(\frac{{95}}{{100}}\)
Percentage loss \(= 95\%\)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
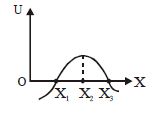
- 1આકૃતિમાં બતાવ્યા અનુસાર, અહી એક કણની સ્થિતિઉર્જા $U$ નો તેના ઉગમબિંદુથી સ્થાન $x$ વિદુદ્ધનો આલેખ દર્શાવેલ છે. નીચેનામાંથી ક્યુ વિધાન સાયું છે. કણ એView Solution
- 2$1250 kg$ ની કાર $30m/s$ ના વેગથી ગતિ કરે છે.$750N$ નું અવરોધક બળ લાગે છે.જો એન્જિન $30kW$ પાવર ઉત્પન્ન કરે,તો કારનો પ્રવેગ કેટલા ............... $\mathrm{m} / \mathrm{s} ^{2}$ થાય?View Solution
- 3પદાર્થને મુકત કરતાં સ્થિતિઊર્જા $U$ ધટે,ત્યારે તેનો વેગ $v$ છે.તો પદાર્થનું દળView Solution
- 4View Solutionબ્લોકને અચળ પાવરથી ખસેડતા તેને કાપેલ અંતર સમયનાં પર કઈ રીતે આધાર રાખે?
- 5$16 N/m$ બળ અચળાંક ધરાવતી સ્પિંગ્ર પર $1 kg$ નો પદાર્થ લટકાવેલ છે.તેને $5 cm$ ખેંચીને મુકતાં તંત્રની ગતિઊર્જા શોધો ?View Solution
- 6એક બોલને $20\,m$ ઊંચાઈએેથી પડવા દેવામાં આવે છે. જો બોલ અને ભોંયતળિયા વચ્ચેના સંઘાત માટેના $restitution$ ગુણાંક $0.5$ છે. ભોંયતળિયા પર અથડાયા બાદ બોલ $.......$ ઉચાઈ સુધી પાછો ફરશે.View Solution
- 7$2\, {kg}$ દળનો પદાર્થ $4\, {m} / {s}$ ના વેગથી ગતિ કરે છે. તે બીજા સ્થિર પડેલા પદાર્થ સાથે સ્થિતિસ્થાપક સંઘાત કરે છે અને પોતાની મૂળ દિશામાં શરૂઆત કરતાં ચોથા ભાગની ઝડપે ગતિ શરૂ રાખે છે. બંને પદાર્થના દ્રવ્યમાનકેન્દ્રનો વેગ $\frac{x}{10} \,{m} / {s}$હોય, તો $x$ નું મૂલ્ય કેટલું હશે?View Solution
- 8$l$ લંબાઇના સાદા લોલકને ${90^°}$ સ્થાનાંતર કરી મૂકવામાં આવે છે.સમતોલન સ્થાન માટે દોરીમાં તણાવ કેટલો હોવો જોઈએ?View Solution
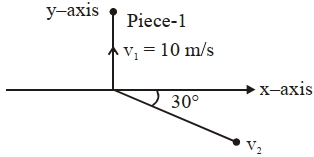
- 9$10\, kg$ નો દડો $10 \sqrt{3} m / s$નાં વેગથી $x-$અક્ષ પર ગતિ કરે છે.તે સ્થિર રહેલા $20\, kg$ના દડાને અથડાતાં તે સ્થિર થાય છે,$20\, kg$નાં દડાના બે ટુકડા થાય છે.એક $10\, kg$નાં ટુકડા $y-$ અક્ષ પર $10$ $m / s$નાં વેગથી ગતિ કરે છે.બીજો $10\, kg$નો ટુકડો $x-$અક્ષ સાથે $30^{\circ}$ નાં ખૂણે $x\, m / s$નાં વેગથી ગતિ કરે છે , તો $x=......$View Solution
- 10જો બે અણું વચ્ચેની સ્થિતિઉર્જાને $U =\frac{-A }{ r ^{6}}+\frac{ B }{ r ^{12}},$ વડે આપવામાં આવે તો સંતુલન સમયે બે અણું વચ્ચેનું અંતર અને સ્થિતિઉર્જા કેટલી હશે?View Solution
