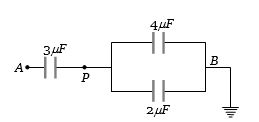
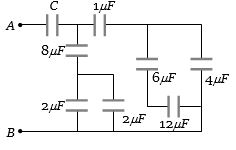
$A$ અને $B$ વચ્ચે સમતુલ્ય કેપેસિટન્સ $1 \,\mu F$ છે.તો $C$ નું મૂલ્ય કેટલું હશે?

Diffcult
d
(d) \(12\, \,\mu F\) and \(6\,\,\mu F\) are in series and again are in parallel with \(4\,\,\mu F\).
Therefore, resultant of these three will be
\( = \frac{{12 \times 6}}{{12 + 6}} + 4 = 4 + 4 = 8\,\mu F\)
This equivalent system is in series with \(1\, \,\mu F\).
Its equivalent capacitance \( = \frac{{8 \times 1}}{{8 + 1}} = \frac{8}{9}\mu F\)\( ....(i)\)
Equivalent of \(8\,\,\mu F,\, 2\,\,\mu F\) and \(2\,\,\mu F\)
\( = \frac{{4 \times 8}}{{4 + 8}} = \frac{{32}}{{12}} = \frac{8}{3}\mu F\)\( .....(ii)\)
\((i)\) and \((ii)\) are in parallel and are in series with \(C\)
\(\frac{8}{9} + \frac{8}{3} = \frac{{32}}{9}\) and \({C_{eq}} = 1 = \frac{{\frac{{32}}{9} \times C}}{{\frac{{32}}{9} + C}}\)
(d) \(12\, \,\mu F\) and \(6\,\,\mu F\) are in series and again are in parallel with \(4\,\,\mu F\).
Therefore, resultant of these three will be
\( = \frac{{12 \times 6}}{{12 + 6}} + 4 = 4 + 4 = 8\,\mu F\)
This equivalent system is in series with \(1\, \,\mu F\).
Its equivalent capacitance \( = \frac{{8 \times 1}}{{8 + 1}} = \frac{8}{9}\mu F\)\( ....(i)\)
Equivalent of \(8\,\,\mu F,\, 2\,\,\mu F\) and \(2\,\,\mu F\)
\( = \frac{{4 \times 8}}{{4 + 8}} = \frac{{32}}{{12}} = \frac{8}{3}\mu F\)\( .....(ii)\)
\((i)\) and \((ii)\) are in parallel and are in series with \(C\)
\(\frac{8}{9} + \frac{8}{3} = \frac{{32}}{9}\) and \({C_{eq}} = 1 = \frac{{\frac{{32}}{9} \times C}}{{\frac{{32}}{9} + C}}\)
\(==>\) \(C = \frac{{32}}{{23}}\,\mu F\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે પ્લેટ વચ્ચેનું અંતર $d$ ધરાવતા સમાંતર પ્લેટ કેપેસીટરમાં $\frac{3}{4} d$ જાડાઈ અને $K$ ડાઈઇલેક્ટ્રિક અચળાંક ધરાવતો સ્લેબ મૂકવામાં આવે છે તો નવો કેપેસીટન્સ $(C')$ અને જૂના કેપેસીટન્સ $\left( C _{0}\right)$ વચ્ચેનો સંબંધ શું થશે?View Solution
- 2$12\,pF$ કેપેસિટન્સ ધરાવતા એક સમાંતર પ્લેટ કેપેસિટરને એક બેટરી વડે તેની બે પ્લેટો વચ્ચે $10\, V$ વિજસ્થિતિમાનના તફાવત સુધી ચાર્જ કરવામાં આવે છે. આ ચાર્જિંગ બેટરીને દૂર કરીને એક પોર્સેલિનના ચોસલા કે જેનો પરાવૈધૃતાંક (dielectric constant) $6.5$ છે તેને આ બે પ્લેટો વચ્ચે સરકાવવામાં આવે છે. આ કેપેસિટર વડે ચોસલા પર કેટલા .......$pJ$ કાર્ય થશે?View Solution
- 3$Q$ વિદ્યુતભાર ધરાવતા એક ધન વાહક ગોળોએ અવિદ્યુતભારીત સમકેન્દ્રિય વાહક ગોળીય કવચની આજુબાજુ આવેલો છે. ધન ગોળીય પૃષ્ઠ અને કવચની બહારના પૃષ્ઠ વચ્ચેનો સ્થિતિમાનનો તફાવત $V$ લો. જો કવચનો વિદ્યુતભાર $-3Q$ હોય તો આ બે સમાન પૃષ્ઠો સ્થિતિમાનનો નવો તફાવત .........$V$ છે.View Solution
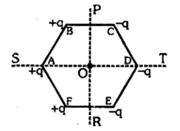
- 4આકૃતિમાં દર્શાવ્યા પ્રમાણે $O$ કેન્દ્ર અને $L$ લંબાઈ બાજુઓના નિયમીત ષષ્ટકોણના શિરોબિંદુઓ આગળ છે. બિંદુવત વિદ્યુતભારો મૂકેલા છે. $K\,\, = \,\,\frac{q}{{4\pi \,\,{ \in _0}\,\,{L^2}}}$, આપેલ છે. નીચેના પૈકી કયું વિધાન સાચું છે ?View Solution
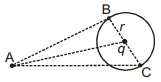
- 5$r$ ત્રિજ્યાવાળા વર્તુળના કેન્દ્ર પર $q$ જેટલો ચાર્જ રાખેલ છે, $B$ અને $C$ બિંદુઓ આ વર્તુંળના પરિઘ પર છે. જ્યારે બિંદુ $A$ આ વર્તુળથી બહાર છે. જો $W_{A B}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $B$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે અને $W_{A C}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $C$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે તો આપેલી આકૃતિ માટે કયું વિધાન સત્ય છે ?View Solution
- 6$10\;cm$ ત્રિજયા ધરાવતા પોલા ગોળાને એવી રીતે વિદ્યુતભારિત કરવામાં આવે છે કે જેથી તેની સપાટી પરનું સ્થિતિમાન $80\;V$ થાય. ગોળાના કેન્દ્ર પર સ્થિતિમાન કેટલું હશે?View Solution
- 7સમાન લંબાઈની દોરીઓ વડે બે એકસમાન વિદ્યુતભારિત ગોળાઓને લટકાવવામાં આવેલા છે. દોરીઓ એકબીજા સાથે $37^{\circ}$ નો કોણ બનાવે છે. જ્યારે $0.7 \mathrm{~g} / \mathrm{cm}^3$ ની ધનતા ધરાવતા પ્રવાહીમાં અંદર લટકાવવામાં આવે છે ત્યારે કોણ સમાન રહે છે. જો ગોળાના દ્રવ્યની ધનતા $1.4 \mathrm{~g} / \mathrm{cm}^3$ હોય તો પ્રવાહીનો ડાઈઇલેકિટ્ર અચળાંક_________થશે.$\left(\tan 37^{\circ}=\frac{3}{4}\right)$View Solution
- 8વિધુતભાર $Q$ ને $a, b, c (a < b < c)$ ત્રિજ્યા ધરાવતા સમકેન્દ્રિય ગોલીય કવચો પર એવી રીતે વહેંચવામાં આવેલ છે કે જેથી તેમની પૃષ્ઠ વિદ્યુતભાર ધનતા એક બીજા જેટલી સમાન થાય. તેમના સામાન્ય કેન્દ્રથી $r$ અંતરે રહેલા બિંદુ, જ્યાં $r < a$, આગળ કુલ સ્થિતિમાન કેટલું હશે?View Solution
- 9$\alpha - $કણ $70\ V$ થી $50\ V$ વોલ્ટેજ ધરાવતાં બિંદુ પર જતાં ગતિઊર્જા કેટલી થાય?View Solution
- 10આકૃતીમાં દર્શાવ્યા મુજબ $A$ બિંદુ આગળ $+1200\, V$ વિદ્યુત સ્થીતીમાન આપેલ છે તથા $B$ બિંદુને શૂન્ય સ્થીતીમાને રાખેલ છે. તો $P$ બિંદુ આગળ વિદ્યુત સ્થીતીમાન.....$V$View Solution