$a$ બાજુવાળા ચોરસ ના શિરોબંદુ પર $+Q$ વિદ્યુતભાર મૂકેલા છે.તો એક વિદ્યુતભાર પર કેટલું બળ લાગે?
Diffcult
Download our app for free and get started
c
\({F_{net}} = {F_{AC}} + {F_D} = \sqrt {F_A^2 + F_C^2 + } {F_D}\)
\({F_{net}} = {F_{AC}} + {F_D} = \sqrt {F_A^2 + F_C^2 + } {F_D}\)
\({F_A} = {F_C} = \frac{{k{Q^2}}}{{{a^2}}}\), \({F_D} = \frac{{k{Q^2}}}{{{{(a\sqrt 2 )}^2}}}\)\({F_{net}} = \frac{{\sqrt 2 k{Q^2}}}{{{a^2}}} + \frac{{k{Q^2}}}{{2{a^2}}} = \frac{{k{Q^2}}}{{{a^2}}}\left( {\sqrt 2 + \frac{1}{2}} \right)\)
\( = \frac{{{Q^2}}}{{4\pi {\varepsilon _0}{a^2}}}\left( {\frac{{1 + 2\sqrt 2 }}{2}} \right)\)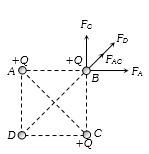
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$1$ કુલંબનો વિદ્યુતભાર $10 \,cm$ ત્રિજ્યાના ગોળાના અને $20 \,cm$ બાજુના સમઘનના કેન્દ્ર પાસે રહેલો છે. ગોળા અને સમઘનમાંથી બહાર જતા ફલક્સનો ગુણોત્તરView Solution
- 2એક વિદ્યુત ડાયપોલ, $2 \,cm$ અંતરે દૂર $1 \,\mu C$ માત્રાના બે વિરૂધ્ધ વિદ્યુતભારોની બનેલી છે. આ ડાયપોલને $10^5\,N/C$ ના બાહ્ય ક્ષેત્રમાં મૂકવામાં આવી છે. ડાયપોલ પર લાગતું મહત્તમ ટોર્ક .......... $Nm$View Solution
- 3$10^{-6}\, kg$ દળના પાણીની ટીપા પરનો વિદ્યુતભાર $10^{-6}\,C$ છે. ટીપા પર કેટલી માત્રાનું વિદ્યુતક્ષેત્ર લાગુ પાડવામાં આવે કે જેથી તે તેના વજન સાથે સંતુલિત અવસ્થામાં હોય.View Solution
- 4ડાઈપોલ માટે $q = 2 × 10^{-6}\ C ; d = 0.01\ m$ જો $E = 5 ×10^{5}\ N/C $ હોય તો ડાઈપોલ પર લાગતું મહત્તમ ટોર્ક શોધો.View Solution
- 5View Solutionઆકૃતિ વિદ્યુતક્ષેત્ર સાથે (સંલગ્ન) કેટલીક વિદ્યુત રેખાઓ દર્શાવે છે. તો......
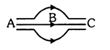
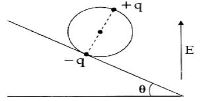
- 6$m $ દળના એક પૈડા પર વ્યાસના બે વિરુધ્ધ બિંદુઓ પર $+q$ અને $ -q$ વિદ્યુતભાર છે. એક ખરબચડા ઢળતા પાટિયા પર શિરોલંબ વિદ્યુતક્ષેત્ર $E$ ની હાજરીમાં તે સંતુલનમાં રહે છે. તો $E$ નું મૂલ્યView Solution
- 7$\varepsilon$$_r$ નું પારિમાણિક સૂત્ર.......View Solution
- 8View Solutionવિદ્યુત ડાઈપોલની વિષુવ રેખા પરના એક બિંદુ માટે વિદ્યુતક્ષેત્રની તીવ્રતાની દિશા ....... છે.
- 9નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન $-I$ : એક બિંદુવત વિદ્યુતભારને વિદ્યુતક્ષેત્રમાં લાવવામાં આવે છે. જો વિદ્યુતભાર ધન હશે તો વિદ્યુતભારની નજીકના બિંદુ આગળ વિદ્યુતક્ષેત્ર વધશે.
વિધાન $-II$ : એક વિદ્યુત દ્વિ-ધ્રુવીને અસમાન (અનિયમિત) વિદ્યુત ક્ષેત્રમાં મૂકવામાં આવેછે. દ્વિ-ધ્રુવી પર સમાસ (પરિણામી) બળ કદાપિ શૂન્ય નહી થાય.
નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો.
- 10ઉગમબિંદુ $(0,0,0)$ આગળ રહેલ એક વિદ્યુત ડાયપોલની ડાયપોલ મોમેન્ટ $\overrightarrow{\mathrm{p}}=(-\hat{\mathrm{i}}-3 \hat{\mathrm{j}}+2 \hat{\mathrm{k}}) \times 10^{-29}\; \mathrm{C} \cdot \mathrm{m}$ છે.ડાયપોલને કારણે $\overrightarrow{\mathrm{r}}=+\hat{\mathrm{i}}+3 \hat{\mathrm{j}}+5 \hat{\mathrm{k}}$ આગળ રહેલ વિદ્યુતક્ષેત્ર કોને સમાંતર હોય? ($\overrightarrow{\mathrm{r}} \cdot \overrightarrow{\mathrm{p}}=0)$View Solution