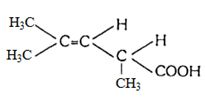
આ પરમાણુ કેટલા અવકાશીય સમઘટ્ક ધરાવે છે
$CH_3CH=CHCH_2CHBrCH_3$
AIPMT 2008, Advanced
Download our app for free and get started
c
\(C^{*}=\) asymmetric carbon
\(C^{*}=\) asymmetric carbon
Number of optical isomers \(=2^{n}\)
where, \(n=\) number of asymmetric carbon atoms
\(2^{1}=2\)
Number of geometrical isomers \(=2^{n}\) where, \(n=\) number of double bonds \(=2^{1}=2\)
Hence, total number of stereoisomers = Total optical isomers \(4 -\) Total geometrical isomers
\(=2+2=4\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1આપેલ પદાર્થ સાચું $IUPAC $ નામ શું છે ?View Solution
$\mathop C\limits_{\mathop |\limits_{COOH} } {H_2}\, - \,\,\mathop {\mathop C\limits^{\mathop |\limits^{OH} } }\limits_{\mathop |\limits_{COOH} } \,\, - \,\,C{H_2}\,\, - \,\,\mathop C\limits_{\mathop {||}\limits_O } \,\, - \,\,OH$
- 2નીચેનામાંથી કયું એ $2,3$ - બ્યુટેનડાયોલ નું મેસો બંધારણ નથી ?View Solution
- 3$2-$ Chloro $-4-$ methylhex $-2-$ ene ના અવકાશ સમઘટકોની સંખ્યા .............View Solution
- 4View Solutionનીચેનું સંયોજન શું પ્રદર્શિત કરી શકે છે?
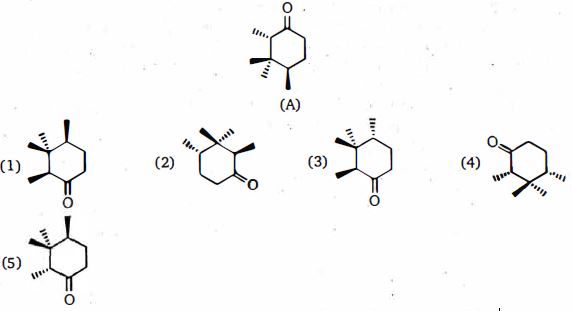
- 5$A$ ના ડાયસ્ટીરિયોમર્સ કઇ રચનાઓ છે ?View Solution
- 6View Solutionનીચેનામાંથી ક્યુ ભૌમિતિક સમઘટકતા દર્શાવતું નથી ?
- 7$C{H_3}CH\left( {COOH} \right) - CH\left( {COOH} \right) - C{H_2}C{H_3}$ સંયોજનના કેટલા પ્રકાશ સમઘટકો શક્ય છે ?View Solution
- 8$(i)$ અને $(ii)$ માટે અનુક્રમે કયા વિન્યાસ જોવા મળે છે ?View Solution
- 9નીચેના કયા એમિનો એસિડ્સમાં, $(R)$ - ઈનાસ્યોમર્સ દ્વારા રજૂ થાય છેView Solution
- 10View Solutionબંધારણ શું દર્શાવે છે ?
