આ સંયોજનોના હાઇડ્રોજનની ઉષ્મા માટે નીચેનામાંથી કયા ક્રમ યોગ્ય છે?
Medium
Download our app for free and get started
c
\((c)\) Heat of hydrogenation \(\propto \, \frac{1}{stability \,of \,alkene}\)
\((c)\) Heat of hydrogenation \(\propto \, \frac{1}{stability \,of \,alkene}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$EAS$ (ઇલેક્ટ્રોન અનુરાગી વિસ્થાપન ) નો દર નો ક્રમ કયો છેView Solution
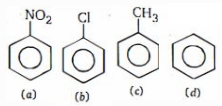
- 2સૂચવેલા મુજબ, $C = C$ બંધ વિશે પરિભ્રમણ અવરોધના નીચેનામાંથી કયા ક્રમ યોગ્ય છે?View Solution
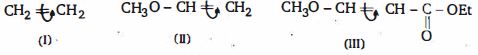
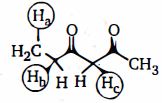
- 3હાઈડ્રોજન અણુઓને ક્રમ આપો $(H_a, H_b, H_c)$ તેમની એસિડિક પ્રબળતાના ક્રમમાં નીચેના કયા અણુમાં હાજર છે.View Solution
- 4View Solutionઆપેલ અણુની સૌથી સ્થાયી પ્રમાણભૂત રચના કઈ છે:
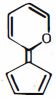
- 5એ.....View Solution
$\begin{matrix}
\overset{\Theta }{\mathop{\overset{\centerdot \,\centerdot }{\mathop{C}}\,}}\,{{H}_{2}}-C-C{{H}_{3}} \\
|| \\
O \\
\end{matrix}$ અને $\begin{matrix}
C{{H}_{2}}=C-C{{H}_{3}} \\
| \\
:\underset{\Theta }{\mathop{\underset{\centerdot \,\centerdot }{\mathop{O}}\,}}\,: \\
\end{matrix}$ - 6$D\,(+)$ $- 2-$ક્લોરો$-2-$ફિનાઇલ ઇથેનનું ટોલ્યુઇનમાં દ્રાવણ, $SbC{l_5}$ની ઓછી માત્રાની હાજરીમાં શું બનાવીને રેસેમીકૃત બને છે?View Solution
- 7નીચે બે વિધાનો આપવામાં આવ્યા છે:View Solution
વિધાન $I : C _{2} H _{5} OH$ અને $AgCN$ બંને કેન્દ્રાનુરાગી ઉત્પન્ન કરી શકે છે.
વિધાન $II : KCN$ અને $AgCN$ બંને બધી પ્રક્રિયાની પરિસ્થિતિઓ સાથે નાઇટ્રિલ કેન્દ્રાનુરાગી ઉત્પન્ન કરશે.
સૌથી યોગ્ય વિકલ્પ પસંદ કરો:
- 8$R_3C-, R_2N-, RO,$ અને $ F^-$ ની કેન્દ્રાનુરાગી માટે ઘટતો ક્રમ કયો છે ?View Solution
- 9આયનીકરણની સ્થિરતાનો ક્રમ કયો છે?View Solution
${\rm{(X)}}{\rm{. }}C{H_3} - \,\,\,\mathop C\limits^ \oplus H\,\, - \,\,C{H_3}$
${\rm{(Y)}}{\rm{. }}C{H_3} - \,\,\,\mathop C\limits^ \oplus H\,\, - \,\,O\,C{H_3}$
${\rm{(Z)}}{\rm{. }}C{H_3} - \,\,\,\mathop C\limits^ \oplus H\,\, - \,\,CO\,C{H_3}$
- 10$- M$ અને ઋણ પ્રેરક અસરોના અસ્તિત્વ માટે વિસ્થાપીત સમૂહોનો યોગ્ય સેટ પસંદ કરો.View Solution