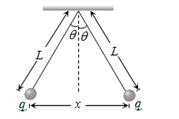
આકૃતીમાં દર્શાવ્યા મુજબ બે નાના, સમાન દળ $m$ અને સમાન વિદ્યુતભાર $q$ ધરાવતા બોલને સમાન લંબાઇ $L$ ધરાવતી અવાહક દોરી વડે લટકાવેલ છે ધારોકે ઘણો નાનો છે કે જેથી $tan\theta \approx sin\theta $ , તો સંતુલન સમયે $x$ = .....

Medium
a
સંતુલનમાં \(F_e = T\, sin\theta ....... (i) \,\, ⇒ mg = T\, cos\theta ....... (ii)\)
સંતુલનમાં \(F_e = T\, sin\theta ....... (i) \,\, ⇒ mg = T\, cos\theta ....... (ii)\)
\(\tan \theta = \frac{{{F_e}}}{{mg}} = \frac{{{q^2}}}{{4\pi {\varepsilon _o}{x^2} \times mg}}\) તથા \(\tan \theta \approx \sin \theta = \frac{{x/2}}{L}\)
માટે \(\frac{x}{{2L}} = \frac{{{q^2}}}{{4\pi {\varepsilon _o}{x^2} \times mg}}\,\, \Rightarrow \,\,{x^3} = \frac{{2{q^2}L}}{{4\pi {\varepsilon _o}mg}}\,\,\, \Rightarrow \,\,x = {\left( {\frac{{{q^2}L}}{{2\pi {\varepsilon _o}mg}}} \right)^{1/3}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionઆકૃતિ વિદ્યુતક્ષેત્ર સાથે (સંલગ્ન) કેટલીક વિદ્યુત રેખાઓ દર્શાવે છે. તો......
- 2$R$ ત્રિજયા ધરાવતા વિદ્યુતભારીત વાહક ગોળીય કવચના કેન્દ્રથી $\frac{{3R}}{2}$ અંતરે વિદ્યુતક્ષેત્ર $E\; V/m$ છે. તેના કેન્દ્રથી $\frac{R}{2}$ અંતરે વિદ્યુતક્ષેત્ર કેટલું થાય?View Solution
- 3સમાન વિદ્યુતભાર ધરાવતા બે સમાન ગોળાઓને એક આધારબિંદુથી સરખી લંબાઈની દોરી વડે લટકાવેલ છે. ત્યારે બે દોરી વચ્ચેનો કોણ $30^o$ છે. જ્યારે $0.8\, g\, cm^{-3}$ ઘનતાના પ્રવાહીમાં ડૂબાડવામાં આવે ત્યારે બે દોરી વચ્ચેનો કોણ ગોળાઓ હવામાં હતા તયારે જેટલો હતો તેટલો જ રહે છે. જો ગોળાઓના દ્રવ્યની ઘનતા $1.6 \,g \,cm^{-3}$ હોય તો પ્રવાહીનો ડાઈઈલેક્ટ્રિક અચળાંક ........ છે.View Solution
- 4$4.9 \times 10^{5} \;N / C$ મૂલ્ય ધરાવતું શિરોલંબ વિદ્યુતક્ષેત્ર, $0.1 \,g$ દળ ધરાવતા પાણીના બુંદને નીચે પડતું આટકાવવા પૂરતું છે. બુંદ પરનો વિધુતભાર........$ \times 10^{-9} \;C$ હશેView Solution
[$g =9.8 \,m / s ^{2}$ આપેલા ]
- 5$1$ $\mu$$C$ અને $5$ $\mu$$C$ ના બે વિદ્યુતભારો $4\, cm$ દૂર આવેલા છે. બંને વિદ્યુતભારો એકબીજા પર લાગતા બળનો ગુણોત્તર....... હશે.View Solution
- 6$100 \,mg$ ના એક વિદ્યુતભારિત કણને $1 \times 10^{5} \,NC ^{-1}$ જેટલી તીવ્રતા ધરાવતા નિયમિત વિદ્યુતક્ષેત્રની વિરૂદધ દિશામાં ફેકવામાં આવે છે. જે કણ પરનો વિદ્યુતભાર $40 \,\mu C$ અને પ્રારંભિક વેગ $200 \,ms ^{-1}$ હોય તો તે ક્ષણિક વિરામસ્થિતિમાં આવતા પહેલા કેટલું અંતર ($m$ માં) કાપ્શે?View Solution
- 7View Solutionપોલરાઈઝેશનની તીવ્રતાનું પારિમાણિક સૂત્ર કયું છે?
- 8બે વિદ્યુતભાર $+8q$ અને $-2q$ ને $x=0$ અને $x=L$ મુકતાં વિદ્યુતક્ષેત્ર કયાં બિંદુએ શૂન્ય થશે?View Solution
- 9ઉગમબિંદુ $O$ આગળ તેના કેન્દ્ર સાથે $X - Y$ સમતલમાં $R$ ત્રિજ્યાની ધન વિદ્યુતભારીત પાતળી ધાતુની રીંગ નિયત કરેલી છે. બિંદુ $(0, 0, Z_0)$ આગળ એક ઋણ વિદ્યુતભારીત કણ $P$ ને સ્થિર સ્થિતિએથી છોડવામાં આવે છે. જ્યાં $(Z_0 > 0)$ તો ગતિ છે.View Solution
- 10View Solutionહાઇડ્રોજન જેવા તંત્રમાં, ઇલેક્ટ્રોન અને પ્રોટોન વચ્ચેનાં કુલ્મબિય બળ અને ગુરુત્વકર્ષણ બળનો ગુણોત્તર . . . . .ના ક્રમનો હોય છે.
