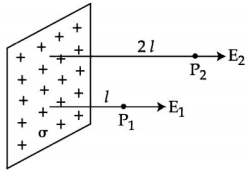
આકૃતિમાં એક ખૂબ મોટું ધન વિદ્યુતભારિત સમતલ પૃષ્ઠ દર્શાવેલ છે. $P _{1}$ અને $P _{2}$ એ વિદ્યુતભાર વિતરણથી $l$ અને $2 l$ જેટલા લઘુત્તમ અંતરે બે બિંદુુઓ છે. જે પૃષ્ઠ વીજભાર ઘનતા $\sigma$ હોય, તો $P_{1}$ અને $P_{2}$ આગળ વિદ્યુતક્ષેત્ર $E_{1}$ અને $E_{2}$ માટે સાચો વિકલ્પ પસંદ કરો

JEE MAIN 2022, Medium
c
As the sheet is very large \(\overrightarrow{ E }\) is independent of distance from it.
As the sheet is very large \(\overrightarrow{ E }\) is independent of distance from it.
Thus \(E _{1}= E _{2}=\frac{\sigma}{2 \varepsilon_{0}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ઉગમબિંદુ પર કેન્દ્ર રહે તેમ વિધુતડાઇપોલ $X$- અક્ષ પર મુકેલ છે. $OP$ રેખા $x$-અક્ષ સાથે $\theta$ ખૂણો બનાવે છે.જો $P$ બિદું આગળ વિધુતક્ષેત્ર $y$- અક્ષની દિશામા હોય તો $\theta$ નું મૂલ્ય કેટલું થાય?View Solution
- 2$e$ વિદ્યુતભાર ધરાવતો અને $m$ દળ ધરાવતો ઇલેક્ટ્રોનને સમાન વિદ્યુતક્ષેત્ર $E$ માં મૂકવામાં આવે તો તેનો પ્રવેગ કેટલો થશે?View Solution
- 3બે સમાન અને $-q$ ઋણ વિદ્યુતભારીત વિદ્યુતભારોને $Y$ અક્ષ પર $(0, a)$ અને $(0, -a)$ બિંદુ આગળ મૂકેલા છે એક ધન વિદ્યુતભાર $q$ સ્થિર સ્થિતિએ છે જે $(2a, 0)$ બિંદુથી ડાબી બાજુએ ગતિ કરે છે. આ વિદ્યુતભાર કયો હશે ?View Solution
- 4$0.5\, m$ ત્રિજ્યાની અર્ધ વર્તૂળ રીંગ કુલ વિદ્યુતભાર $1.4 \times 10^{-9}\, C$ થી સમાન વિદ્યુતભારીત કરેલ છે. રીંગના કેન્દ્ર આગળ વિદ્યુતક્ષેત્રની તીવ્રતા ........$V/m$ છે.View Solution
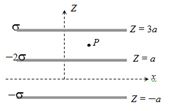
- 5આકૃતીમાં દર્શાવ્યા મુજબ ત્રણ અનંત લંબાઇથી પ્લેટોને મુકેલ છે તો $P$ બિંદુ આગળ વિદ્યુત ક્ષેત્ર....View Solution
- 6બે સમાન મૂલ્યના $q$ વિદ્યુતભારો $x$ અક્ષ પર $2a$ અંતરે આવેલા છે. $m$ દળના બીજો $q$ વિદ્યુતભારને બે વિદ્યુતભારની વચ્ચેના માર્ગ (પથ) પર મૂકેલ છે. જો આ વિદ્યુતભાર સમતુલન સ્થિતિથી $x$ અંતરે સ્થાન બદલે તો કણ .........View Solution
- 7સમાન વિદ્યુતભાર ધરાવતા,સમાન ગોળા $A$ અને $B$ વચ્ચે લાગતું અપાકષૅણ બળ $F$ છે.હવે વિદ્યુતભાર રહિત ગોળો $C$ ને $A$ સાથે સંપર્ક કરાવીને ગોળા $A$ અને $B$ ની મધ્યમાં મૂકતાં તેના પર કેટલું બળ લાગે?View Solution
- 8View Solutionપદાર્થ ઋણ વિજભારિત ક્યારે થશે?
- 9$+8q$ અને $-2q$ બિંદુવત વિદ્યુતભારો $x = 0$ અને $x = L$ પાસે મૂકેલાં છે. તો $X -$ અક્ષ પરના કયા બિંદુ આગળ પરિણામી વિદ્યુતક્ષેત્રની તીવ્રતા શૂન્ય થશે?View Solution
- 10બે બિંદુગત વિદ્યુતભારો $e$ અને $3 e$ ને $r$ અંતરે મૂકવામાં આવ્યા છે. વિદ્યુતભારથી કેટલા અંતરે વિદ્યુતક્ષેત્ર તીવ્રતા શૂન્ય હશે ?View Solution
