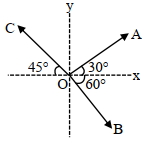
Let magnitude be equal to \(\lambda\).
\(\overrightarrow{ OA }=\lambda\left[\cos 30^{\circ} \hat{ i }+\sin 30 \hat{ j }\right]=\lambda\left[\frac{\sqrt{3}}{2} \hat{ i }+\frac{1}{2} \hat{ j }\right]\)
\(\overrightarrow{ OB }=\lambda\left[\cos 60^{\circ} \hat{ i }-\sin 60 \hat{ j }\right]=\lambda\left[\frac{1}{2} \hat{ i }-\frac{\sqrt{3}}{2} \hat{ j }\right]\)
\(\overrightarrow{ OC }=\lambda\left[\cos 45^{\circ}(-\hat{ i })+\sin 45 \hat{ j }\right]=\lambda\left[-\frac{1}{\sqrt{2}} \hat{ i }+\frac{1}{\sqrt{2}} \hat{ j }\right]\)
\(\therefore \overrightarrow{ OA }+\overrightarrow{ OB }-\overrightarrow{ OC }\)
\(=\lambda\left[\left(\frac{\sqrt{3}+1}{2}+\frac{1}{\sqrt{2}}\right) \hat{ i }+\left(\frac{1}{2}-\frac{\sqrt{3}}{2}-\frac{1}{\sqrt{2}}\right) \hat{ j }\right]\)
\(\therefore\) Angle with \(x\)-axis
\(\tan ^{-1}\left[\frac{\frac{1}{2}-\frac{\sqrt{3}}{2}-\frac{1}{\sqrt{2}}}{\frac{\sqrt{3}}{2}+\frac{1}{2}+\frac{1}{\sqrt{2}}}\right]=\tan ^{-1}\left[\frac{\sqrt{2}-\sqrt{6}-2}{\sqrt{6}+\sqrt{2}+2}\right]\)
\(=\tan ^{-1}\left[\frac{1-\sqrt{3}-\sqrt{2}}{\sqrt{3}+1+\sqrt{2}}\right]\)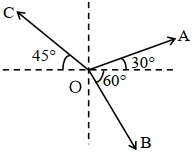
Download our appand get started for free
Similar Questions
- 1View Solutionપરિણામી અદિશનું મૂલ્ય શૂન્ય મેળવવા માટે સમાન મૂલ્યના ઓછામાં ઓછા કેટલા સદિશ જરૂરી છે?
- 2$P, Q$ અને $R$ સદિશો એક બિંદુ પર લાગે છે,તે બિંદુ સમતોલનમાં છે. જો $P = 1.9318\, kg\, wt, \, \sin {\theta _1} = 0.9659,\,$ હોય તો $R =$ ______ ( in $kg wt$)View Solution
- 3સદિશો $ \overrightarrow A = 3\hat i - 6\hat j + 2\hat k $ અને $ \overrightarrow B = 2\hat i + \hat j - 2\hat k $ બનતા ત્રિકોણનું ક્ષેત્રફળ કેટલું થશે?View Solution
- 4સમાંતરફલકની બાજુઓ $\hat i\,\, + \;\,2\hat j,\,\,4\hat j,\,\,\hat j\,\, + \;\,3\hat k$ સદિશની મદદથી દર્શાવેલ છે. તો તેનું કદ શોધો.View Solution
- 5જો $| A + B |=| A |+| B |$ હોય તો સદિશ $ \overrightarrow A $ અને $ \overrightarrow B $ વચ્ચેનો ખૂણો કેટલો હોવો જોઈએ?View Solution
- 6જો બે સદીશોના સરવાળાનું મૂલ્ય એ તેમની બાદબાકીના મૂલ્ય બરાબર હોય, તો આ બે સદીશો વચ્ચેનો ખૂણો ($^o$ માં) કેટલો હશે?View Solution
- 7સદિશ $\overrightarrow a $ ને $d\theta $ખૂણે ફેરવતાં $|\Delta \overrightarrow a |$ અને $\Delta a$ મેળવો.View Solution
- 8સદીશ $A=\hat{i}+\hat{j}+\hat{k}$ નો સદીશ $\vec{B}=\hat{i}+\hat{j}$ પરનો પ્રક્ષેપણ શું થાય?View Solution
- 9સદિશ $\mathop A\limits^ \to \,$ અને $ \,\mathop B\limits^ \to $ x-અક્ષની સાપેક્ષે અનુક્રમે $20^0$ અને $110^0$ ખૂણો બનાવે છે. આ સદિશોનું મૂલ્ય અનુક્રમે $5 m$ અને $12 m$ છેતો તેના પરિણામી સદીશે x-અક્ષ સાથે રચાતા ખૂણાનું મૂલ્ય ..... મળેે.View Solution
- 10એક પ્લેન $100 \,km/hr$ ની ઝડપથી પૃથ્વીને ફરતે પરિભ્રમણ કરે છે.તે અડધું પરિભ્રમણ કરે,ત્યારે તેના વેગમાં કેટલો ફેરફાર ......... $km/hr$ થાય?View Solution
