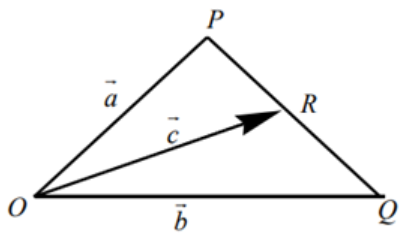
આકૃતિમાં ત્રણ સદિશો$\mathop {\,a}\limits^ \to \,,\,\mathop {\rm{b}}\limits^ \to \,\,$ અને $ \,\mathop {\rm{c}}\limits^ \to \,$આપેલી જ્યાં $R$ એ $PQ$ નું મધ્યબિંદુ છે તો નીચેના પૈકી કયો સંબંધ સાચો છે ?
Medium
Download our app for free and get started
a
Step 1: Applying triangle law of vector addition From triangle law of vector addition,
Step 1: Applying triangle law of vector addition From triangle law of vector addition,
In \(\triangle OPR\)
\(\vec{a}=\vec{c}+\overrightarrow{R P}\)
and \(\operatorname{In} \triangle ORQ\)
\(\overrightarrow{ b }=\overrightarrow{ c }+\overrightarrow{ RQ }\)
Step \(2:\) Equation solving
Adding \(eq ^{ n }(1)\) and (2)
\(\vec{a}+\vec{b}=2 \vec{c}+\overrightarrow{R P}+\overrightarrow{R Q}\)
Since \(R\) is midpoint of \(PQ\), therefore \(\overrightarrow{ RP }=-\overrightarrow{ RQ }\) \(\Rightarrow \vec{a}+\vec{b}=2 \vec{c}+\overrightarrow{R P}-\overrightarrow{R P}\)
\(\Rightarrow \vec{a}+\vec{b}=2 \vec{c}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$ (\overrightarrow P + \overrightarrow Q ) $ અને $ (\overrightarrow P \times \overrightarrow Q ) $ વચ્ચે ખૂણો કેટલો હશે?View Solution
- 2જો $\mathop {\,{\rm{A}}}\limits^ \to \,\, + \;\,\mathop {\rm{B}}\limits^ \to \,\, = \,\mathop {\rm{C}}\limits^ \to $ અને $ {\rm{A}}\,\, + \;\,{\rm{B}}\,\, = \,\,{\rm{C}}\,$ હોય $\vec A $ અને $\vec B $ વચ્ચેનો ખૂણો કેટલો થાય .View Solution
- 3$3P$ અને $2P$ નું પરિણામી $R$ છે.જો પ્રથમ બળ બમણું કરતાં પરિણામી બમણું થાય,તો બંને બળ વચ્ચેનો ખૂણો ........... $^o$ હશે.View Solution
- 4સ્થિર અવસ્થામાં રહેલો પદાર્થ પર ત્રણ બળ સદીશ $2 \hat{i}+2 \hat{j}, 2 \hat{i}-2 \hat{j}$ અને $-4 \hat{i}$ દ્વારા લગાવવામાં આવે છે. તો પદાર્થ કઈ દિશામાં ગતિ કરશે?View Solution
- 5સમાંતર બાજુ ચતુષ્કોણ કે જેના વિકર્ણો ${3\hat i}\,\, + \,\,\hat j\,\, - \,\,2\hat k$ અને $\hat i\,\, - \,\,3\hat j\,\, + \;\,4\hat k$ છે. તો તેનું ક્ષેત્રફળ શોધો.View Solution
- 6View Solutionજો બે સમાન મૂલ્યના બળો કોઈ પદાર્થ પર પૂર્વ અને ઉત્તર દિશામાં લગાવવામાં આવે તો....
- 7બે સદીશ ${\overrightarrow F _1} = 2\hat i + 5\hat k$ અને ${\overrightarrow F _2} = 3\hat j + 4\hat k$ ના અદિશ ગુણાકારનું મૂલ્ય કેટલું મળે?View Solution
- 8જો $\overrightarrow A \times \overrightarrow B=\overrightarrow B \times \overrightarrow A$ , તો $ \overrightarrow A $ અને $ \overrightarrow B $ વચ્ચેનો ખૂણો કેટલો હશે?View Solution
- 9ધારોકે $\vec{A}=2 \hat{i}-3 \hat{j}+4 \hat{k}$ અને $\vec{B}=4 \hat{i}+\hat{j}+2 \hat{k}$ છે તો $|\vec{A} \times \vec{B}|=$View Solution
- 10સ્થિર અવસ્થામાં રહેલો પદાર્થ પર ત્રણ બળ સદીશ $2 \hat{i}+2 \hat{j}, 2 \hat{i}-2 \hat{j}$ અને $-4 \hat{i}$ દ્વારા લગાવવામાં આવે છે. તો પદાર્થ કઈ દિશામાં ગતિ કરશે?View Solution