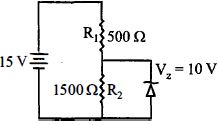
The voltage drop across \(\mathrm{R}_{2}\) is \(\mathrm{V}_{\mathrm{R}_{2}}\) \(=\mathrm{V}_{\mathrm{Z}}=10 \mathrm{V}\)
The current through \(\mathrm{R}_{2}\) is
\(\mathrm{I}_{\mathrm{R}_{2}}=\) \(\frac{\mathrm{V}_{\mathrm{R}_{2}}}{\mathrm{R}_{2}}\) \(=\frac{10 \mathrm{V}}{1500 \Omega}\) \(=0.667 \times 10^{-2} \mathrm{A}\)
\(=6.67 \times 10^{-3} \mathrm{A}=6.67 \mathrm{mA}\)
The voltage drop across \(R_{1}\) is
\(\mathrm{V}_{\mathrm{R}_{1}}=15 \mathrm{V}-\mathrm{V}_{\mathrm{R}_{2}}\) \(=15 \mathrm{V}-10 \mathrm{V}=5 \mathrm{V}\)
The current through \(\mathrm{R}_{1}\) is
\(\mathrm{I}_{\mathrm{R}_{1}}=\frac{\mathrm{V}_{\mathrm{R}_{1}}}{\mathrm{R}_{1}}=\frac{5 \mathrm{V}}{500 \Omega}=10^{-2} \mathrm{A}=10 \times 10^{-3} \mathrm{A}=10 \mathrm{mA}\)
The current through the zener diode is
\(\mathrm{I}_{\mathrm{Z}}=\mathrm{I}_{\mathrm{R}_{1}}-\mathrm{I}_{\mathrm{R}_{2}}\) \(=(10-6.67) \mathrm{mA}=3.3 \mathrm{mA}\)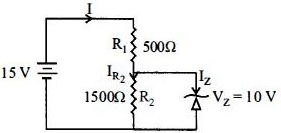
Download our appand get started for free
Similar Questions
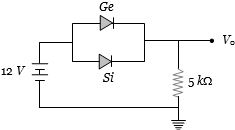
- 1સિલિકોન $Si$ અને જર્મેનિયમ $ Ge$ ડાયોડના કટ-ઇન વોલ્ટેજ અનુક્રમે $0.7 V $ અને $0.3 V$ છે.જર્મેનિયમ ડાયોડને ઉલટાવવાથી $V_o$ માં કેટલા ....$V$ ફેરફાર થાય?View Solution
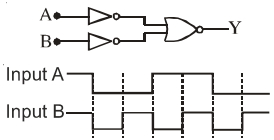
- 2આકૃતિમાં દર્શાવેલ લોજિક પરિપથ માટે ઇનપુટ $A$ અને $B$ ના તરંગો દર્શાવેલ છે.કયો વિકલ્પ આઉટપુટ તરંગ દર્શાવે છે?View Solution
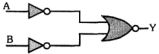
- 3View Solutionનીચે આપેલ લોજીક ગેટ સંજ્ઞા (મિશ્રણ લોજીક ગેટ) દર્શાવે છે ?
- 4જ્યારે $2480 nm$ જેટલી મહત્તમ તરંગલંબાઈનું વિદ્યુતચુંબકીય વિકિરણ આપાત કરતા આપેલા અર્ધવાહકની વિદ્યુતવાહકતા વધે છે. આ અર્ધવાહકની બૅન્ડગૅપ ($eV$ માં) .......View Solution
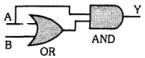
- 5View Solutionનીચે દર્શાવેલ ગેટ્સના જોડાણોનું આઉટપુટ કેટલું થશે?
- 6View Solutionનીચા તાપમાને શેમાં વેલેન્સ બેન્ડ અને કન્ડકટન્સ બેન્ડ ઓવરલેપ હોય છે?
- 7$OR$ ગેટનું આઉટપુટ $NAND$ ગેટનાં બંને ઈનપુટ સાથે જોડેલાં છે. આ જોડાણ નીચેના ગેટ જેવું જ કામ આપશે.View Solution
- 8View Solutionટ્રાન્ઝિસ્ટરને સ્વીચ (કળ) તરીક વાપરવા માટે તેને .............. જ કાર્યરત કરવું પડશે.
- 9View Solutionમુક્ત ઇલેક્ટ્રોનની મોબીલીટી મુક્ત હોલ કરતાં વધું છે કારણ કે
- 10View Solutionડેપ્લેશન સ્તરમાં ....... હોય છે.
