\(\overrightarrow{\mathrm{E}}=\mathrm{E}_{0} \hat{\mathrm{i}}+2 \mathrm{E}_{0} \hat{\mathrm{j}}\)
Given, \(\mathrm{E}_{0}=100 \,\mathrm{N} / \mathrm{c}\)
So, \(\overrightarrow{\mathrm{E}}=100 \hat{\mathrm{i}}+200 \hat{\mathrm{j}}\)
Radius of circular surface \(=0.02\, \mathrm{m}\)
Area \(=\pi r^{2}=\frac{22}{7} \times 0.02 \times 0.02\)
\(=1.25 \times 10^{-3} \hat{\mathrm{i}}\, \mathrm{m}^{2}\) [Loop is parallel to \(\mathrm{Y}-\mathrm{Z}\) plane ]
Now, flux \((\phi)=\) \(EA \,cos\) \(\theta\)
\(=(100 \hat{\mathrm{i}}+200 \hat{\mathrm{j}}) \cdot 1.25 \times 10^{-3} \mathrm{i} \cos \theta^{\circ}\left[\theta=0^{\circ}\right]\)
\(=125 \times 10^{-3}\, \mathrm{Nm}^{2} / \mathrm{c}\)
\(=0.125\, \mathrm{Nm}^{2} / \mathrm{c}\)
Download our appand get started for free
Similar Questions
- 1ડાઈપોલ માટે પ્રત્યેક વિદ્યુતભારની કિંમત $10^{-10} \,st\, C$ અને તેમના વચ્ચેનું અંતર $1\,\mathop A\limits^o $ હોય તો તેની ડાઈપોલની ચાકમાત્રા ........ છે.View Solution
- 2નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન $-I$ : એક બિંદુવત વિદ્યુતભારને વિદ્યુતક્ષેત્રમાં લાવવામાં આવે છે. જો વિદ્યુતભાર ધન હશે તો વિદ્યુતભારની નજીકના બિંદુ આગળ વિદ્યુતક્ષેત્ર વધશે.
વિધાન $-II$ : એક વિદ્યુત દ્વિ-ધ્રુવીને અસમાન (અનિયમિત) વિદ્યુત ક્ષેત્રમાં મૂકવામાં આવેછે. દ્વિ-ધ્રુવી પર સમાસ (પરિણામી) બળ કદાપિ શૂન્ય નહી થાય.
નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો.
- 3$R$ ત્રિજ્યા ધરાવતા વાહક ગોળામાં વિધુતભાર સમાન રીતે વિતરિત કરેલ છે તો કેન્દ્ર $x$ અંતર ($x < R$) માટે વિધુતક્ષેત્ર કોના સમપ્રમાણમાં હોય ?View Solution
- 4$p$ ડાયપોલ મોમેન્ટ ધરાવતા ડાયપોલનું કેન્દ્ર ઉદ્ગમબિંદુ પર રહે તે રીતે $x$-અક્ષ પર મૂકેલ છે.ડાયપોલના કેન્દ્રથી અમુક અંતરે આવેલા બિંદુને જોડતી રેખાએ $x$-અક્ષ સાથે બનાવેલો ખૂણો $\theta $ છે.તો તે બિંદુએ વિદ્યુતક્ષેત્રએ $x$-અક્ષ સાથે કેટલો ખૂણો બનાવે? [ $\tan \alpha = \frac{1}{2}\tan \theta $ ]View Solution
- 5બે સમાન મૂલ્યના $q$ વિદ્યુતભારો $x$ અક્ષ પર $2a$ અંતરે આવેલા છે. $m$ દળના બીજો $q$ વિદ્યુતભારને બે વિદ્યુતભારની વચ્ચેના માર્ગ (પથ) પર મૂકેલ છે. જો આ વિદ્યુતભાર સમતુલન સ્થિતિથી $x$ અંતરે સ્થાન બદલે તો કણ .........View Solution
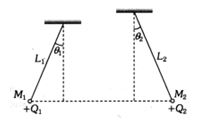
- 6$M_1$ અને $M_2$ દળ ધરાવતા બે નાના ગોળાઓને $L_1$ અને $L_2$ લંબાઇની વજન રહીત અવાહક દોરી વડે લટકાવેલ છે. ગોળાઓ પરનો વિદ્યુતભાર અનુક્રમે $Q_1$ અને $Q_2$ છે. ગોળાઓ એવી રીતે લટકાવેલ છે કે જેથી તેઓ સમક્ષીતીજ એક જ રેખામાં રહે તથા દોરીઓ શીરોલંબ સાથે આકૃતીમાં દર્શાવ્યા મુજબ $\theta_1$ અને $\theta_2$ માપનો ખૂણો બનાવે તો નીચેનામાંથી કઇ શરત $\theta_1$ $=$ $\theta_2$ થવા માટે જરૂરી છે.?View Solution
- 7View Solutionઇલેક્ટ્રીક ડાઈપોલને અસમાન વિધુતક્ષેત્રમાં મુક્તા તે .............. અનુભવે છે
- 8View Solutionનીચેના પૈકી કયો વિદ્યુતભાર મિલ્કનના તેલના ટીપાના પ્રયોગમાં હાજર હોતો નથી?
- 9$10 \,cm$ ત્રિજ્યાના એકરૂપ વિદ્યુતભારીત અવાહક ગોળાના કેન્દ્રથી $20 \,cm$ અંતરે વિદ્યુતક્ષેત્ર $E$ છે. તો $5 \,cm$ અંતરે કેટલું હશે ?View Solution
- 10બે બિંદુગત વિદ્યુતભારો $e$ અને $3 e$ ને $r$ અંતરે મૂકવામાં આવ્યા છે. વિદ્યુતભારથી કેટલા અંતરે વિદ્યુતક્ષેત્ર તીવ્રતા શૂન્ય હશે ?View Solution
