બે બાજુ $A$ અને $A'$ આડછેદની ક્ષેત્રફળ ધરાવતી નળી માથી પાણી વહે છે જ્યાં આડછેદના ક્ષેત્રફળનો ગુણોત્તર $A/A'=5$. જો નળીના બંને છેડા વચ્ચે દબાણનો તફાવત $3 \times 10^5\, N\, m^{-2}$ હોય તો નળીમાં પાણી .......... $m s^{-1}$ ના વેગથી પ્રવેશ કરે?(ગુરુત્વાકર્ષણની અસરને અવગણો)
AIEEE 2012, Diffcult
a
According to \(Bernoulli's\) theorem
According to \(Bernoulli's\) theorem
\({P_1} + \frac{1}{2}\rho v_1^2 = {P_2} + \frac{1}{2}\rho v_2^2\,\,\,...\left( i \right)\)
From question,
\({P_1} - {P_2} = 3 \times {10^5},\frac{{{A_1}}}{{{A_2}}} = 5\)
According to equation of constinuity
\({A_1}{v_1} = {A_2}{v_2}\)
\(or,\frac{{{A_1}}}{{{A_2}}} = \frac{{{v_2}}}{{{v_1}}} = 5\)
\( \Rightarrow \,\,{v_2} = 5{v_1}\)
From equation \((i)\)
\({P_1} - {P_2} = \frac{1}{2}\rho \left( {v_2^2 - v_1^2} \right)\)
\(or\,\,3 \times {10^5} = \frac{1}{2} \times 1000\left( {5v_1^2 - v_1^2} \right.\)
\( \Rightarrow 600 = 6{v_1} \times 4{v_1}\)
\( \Rightarrow v_1^2 = 25\)
\(\therefore \,{v_1} = 5\,m/s\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$20\; m$ ની ઊંચાઈનો નળાકાર સંપૂર્ણપણે પાણીથી ભરેલો છે. તેના તળિયાની નજીક નળાકારની બાજુની દિવાલ પરના નાના છિદ્રમાંથી બહાર આવતા પાણીના પ્રવાહનો વેગ ($ m/s$ માં) કેટલો હશે?View Solution
- 2$a $ ત્રિજયાની કેશનળી વચ્ચે દબાણનો તફાવત $P $ રાખવાથી પ્રવાહીનો વહન દર $Q$ છે.જો $ a/2 $ ત્રિજયા અને $2P $ દબાણ કરવાથી પ્રવાહીના વહન દર કેટલો થાય?View Solution
- 3$2 \,cm$ અને $4\, cm$ ત્રિજયા ધરાવતી બે નળીને શ્રેણીમાં જોડતાં તેમાં પ્રવાહનો ગુણોત્તરView Solution
- 4$d,\,2d$ અને $3d$ ઘનતા ધરાવતા ત્રણ પ્રવાહી સમાન દળ લઇને મિશ્રણ કરવાથી, મિશ્રણની ઘનતા કેટલી થાય?View Solution
- 5$P$ દબાણનો તફાવત ધરાવતી નળીમાં પ્રવાહીનું વહન થાય છે. જો બમણી ત્રિજયા અને બમણી લંબાઇ ધરાવતી નળીમાં બમણા દરથી પ્રવાહીનું વહન કરવા માટે જરૂરી દબાણનો તફાવત કેટલો થાય?View Solution
- 6શ્રેણીમાં જોડેલી સમાન લંબાઇની બે કેશનળીની ત્રિજયાનો ગુણોત્તર $ 1:2 $ છે.તેના બે છેડા વચ્ચે દબાણનો તફાવત $1m$ ઊંચાઇના પાણીના સ્તંભ જેટલો છે.તો પ્રથમ કેશનળી વચ્ચે દબાણનો તફાવત ....... $m$ ઊંચાઇના પાણીના સ્તંભ જેટલો હોય.View Solution
- 7એક ઘરની છત પર રહેલી $750\,cm^{2}$ ક્ષેત્રફળ ધરાવતી પાણીની ટાંકીમાં પાણીનું લેવલ પાઈપ ઉપર નળના સ્તરથી ઊંચે રહેલ છે. $500\,nm^2$ આડછેદનું ક્ષેત્રફળ ધરાવતો નળ જ્યારે ખુલ્લો હોય ત્યારે નળમાંથી બાહર નીકળતા પાણીનો વેગ $30\,cm/s$ છે. આ સમયે $\frac{dh}{dt}$ નું મૂલ્ય $x \times 10^{-3}\,m/s$ છે. $x$ નું મૂલ્ય $...........$ હશે.View Solution
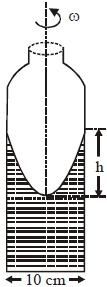
- 8આકૃતિમાં દર્શાવ્યા પ્રમાણે એક નળાકાર પાત્રમાં પ્રવાહી ભરીને તેને પોતાની અક્ષને અનુલક્ષીને ફેરવવામાં આવે છે. પાત્રની ત્રિજ્યા $5\, cm$ અને ભ્રમણની કોણીય ઝડપ $\omega\; rad \,s^{-1}$ છે. પાત્રની વચ્ચે અને પાત્રની સપાટી વચ્ચે ઊંચાઈનો ફેરફાર $h($ $cm$ માં)કેટલો હશે?View Solution
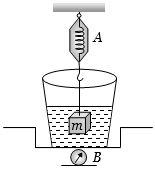
- 9એક સ્પ્રિંગકાંટો $A$ તેની સાથે લટકાવેલ બ્લોક $m$ નું અવલોકન $2\, kg$ દર્શાવે છે. જ્યારે વજનકાંટા $B$ પર મૂકેલું બીકર પ્રવાહીથી ભરવામાં આવે છે ત્યારે તે $5 \,kg $ અવલોકન દર્શાવે છે. આકૃતિ માં દર્શાવ્યા મુજબ લટકાવેલું દળ પ્રવાહીની અંદર રહે તેમ બંને વજનકાંટા ને ગોઠવેલા છે. આ પરિસ્થિતી માં .....View Solution
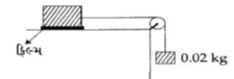
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે જેના પાયાનું ક્ષેત્રફળ $0.2 \;m^2$ હોય, તેવા એક બ્લેાકને $0.02 \;kg$ નું દળ એક દોરી વડે એક આદર્શ ગરગડી પરથી લગાડેલ છે. એક પ્રવાહીનું $0.6\; mm$ જાડાઈનું પાતળું સ્તર આ બ્લોક અને ટેબલ વચ્ચે મૂકવામાં આવે છે. જયારે બ્લોકને છોડવામાં આવે ત્યારે તે $0.17 \;m/s$ ની અચળ ઝડપથી જમણી તરફ ગતિ કરે છે. આ પ્રવાહીનો સ્નિગ્ધતાંક કેટલો હશે?View Solution