\(Young's\,modulus,\,Y = \frac{{Fl}}{{A\Delta l}}\)
Since initial volume of wires are same
\(\therefore \) Their areas of cross sections are \(A\) and \(3A\) and lengths are \(3l\) and \(l\) respectively.
For Wire \(1,\)
\(\Delta l = \left( {\frac{F}{{AY}}} \right)3l\,\) \(...(i)\)
For wire \(2\), let \(F'\) force is applied
\(\frac{{F'}}{{3A}} = Y\frac{{\Delta l}}{l}\)
\( \Rightarrow \Delta l = \left( {\frac{{F'}}{{3AY}}} \right)l\)
From eqns \((i)\) and \((ii),\)
\(\left( {\frac{F}{{AY}}} \right)3l = \left( {\frac{{F'}}{{3AY}}} \right)l \Rightarrow F' = 9F\)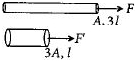
Download our appand get started for free
Similar Questions
- 1તારનો યંગ મોડ્યુલસ $ Y$ અને એકમ કદ દીઠ ઉર્જા $E$ હોય તો વિકૃતિ કેટલી થાય $?$View Solution
- 2View Solutionજો પદાર્થ માટે નાનુ પ્લાસ્ટીક વિરૂ૫ણ હોય તો તે ......
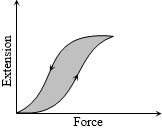
- 3રબર માટે બળ વિરુધ્ધ લંબાઇના વધારાનો આલેખ આપેલ છે.View Solution
$I.$ આ રબરની લંબાઇમાં વધારો-ધટાડો સહેલાઇથી કરી શકાય છે.
$II.$ રબરને ખેંચ્યા પછી તે મૂળ લંબાઇ પ્રાપ્ત કરશે નહિ.
$III.$ રબરને ખેચીને મૂકતાં તે ગરમ થાય છે.
આ આલેખ માટે સાચું વિધાન
- 4View Solutionવિધાન : સમાન પદાર્થમાથી બનાવેલ પોલો નળાકાર નક્કર નળાકાર કરતાં વધારે મજબૂત હોય છે.
કારણ : સમાન લંબાઈ અને પદાર્થમાથી બનાવેલ પોલા નળાકાર ને વાળવા આપવું પડતું ટોર્ક નક્કર નળાકારને વાળવા આપવા પડતાં ટોર્ક કરતાં વધારે હોય
- 5સ્ટીલના સળીયાની ત્રિજ્યા $10 \,mm$ અને લંબાઈ $1.0 \,m$. બળ લાગુ પડત્તા તેમાં ખેંચાણના લીધે $0.32\%$ વિકૃતી ઉદભવે છે. સ્ટીલનો યંગ મોડ્યુલસ $2.0 \times 10^{11} \,Nm ^{-2}$. તો ખેંચાણ દરમીયાન બળની તીવ્રતા .............. $kN$View Solution
- 6$3 \times {10^{ - 6}}\,{m^2}$ આડછેદ અને $4m$ લંબાઇ ધરાવતા તાર પર બળ લગાડતાં લંબાઇમાં થતો વધારો $1\, mm$ છે,તો સંગ્રહીત ઊર્જા કેટલી થાય ? $(Y = 2 \times {10^{11}}\,N/{m^2})$View Solution
- 7આપેલ ઘન પદાર્થ માટે પોઈસન ગુણોતર $\sigma$ કદ સ્થિતિસ્થાપકતા અંક $(K)$ અને દૃઢતા અંક $(\eta)$ વચ્ચેનો સાચો સંબંધ પસંદ કરો:View Solution
- 8બે સમાન સ્ટીલ તથા કોપરના તારને સમાનબળથી ખેંચવામા આવે છે. તેમાં $2 \,cm$ જેટલું સંપૂર્ણ વિસ્તરણ થાય છે તો સ્ટીલ અને કોપરમાં કેટલું વિસ્તરણ થશે ? $Y_{\text {steel }}=20 \times 10^{11} \,dyne / cm ^2$, $Y_{\text {copper }}=12 \times 10^{11} \,dyne / cm ^2$View Solution
- 9ચાર સમાન તાર પર સમાન બળ લગાવવામાં આવે તો મહત્તમ લંબાઈમાં વધારો શેમાં જોવા મળે $?$View Solution
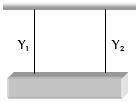
- 10સમાન લંબાઇ અને સમાન આડછેદના ક્ષેત્રફળવાળા બે તારોને આકૃતિમાં બતાવ્યા પ્રમાણે લટકાવ્યા છે. તેમના યંગ મોડયુલસ ${Y_1}$ અને ${Y_2}$ છે. તો તેમનો સમતુલ્ય યંગ મોડયુલસ કેટલો થાય?View Solution