બિંદુ $ (x,y,z) $ (મીટરમાં) આગળનું વિદ્યુતસ્થિતિમાન $ V=4x^2$ $volt$ છે. બિંદુ $(1,0,2)$ આગળ વિદ્યુતક્ષેત્રની તીવ્રતા $(V/m$ માં) ......
AIPMT 2011, Easy
a
\(\vec{E}=-\bar{\nabla} V\)
\(\vec{E}=-\bar{\nabla} V\)
where \(\bar{\nabla}=\hat{i} \frac{\partial}{\partial x}+\hat{j} \frac{\partial}{\partial y}+\hat{k} \frac{\partial}{\partial z}\)
\(\therefore \quad \vec{E}=-\left[\hat{i} \frac{\partial V}{\partial x}+\hat{j} \frac{\partial V}{\partial y}+\hat{k} \frac{\partial V}{\partial z}\right]\)
Here, \(V=4 x^{2} \quad \therefore \quad \vec{E}=-8 x \hat{i}\)
The electric field at point \((1,0,2)\) is
\(\vec{E}_{(1,0,2)}=-8 \hat{i}\,Vm^{-1}\)
So electric field is along the negative \(X\) -axis.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
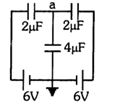
- 1આપેલા પરિપથ માટે, $2\ \mu F$ કેપેસિટર પરનો વોલ્ટેજ શોધો.View Solution
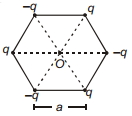
- 2નિયમિત ષટ્કોષનાં શિરોબિંદુઓ પર બિંદુુવત્ વિદ્યુતભારને આકૃતિમાં દર્શાવ્યા મુજબ રાખેલ છે. $O$ ઉગમબિંદુએ $E$ વિદ્યુતક્ષેત્ર દર્શાવતું હોય અને $V$ વિદ્યુત સ્થિતિમાન દર્શાવે છે, તોView Solution
- 3$m$ દળનો બિંદુવત વિદ્યુતભાર $q$ અને $R$ ત્રિજ્યા એ $Q$ વિદ્યુતભાર વાળી રીંગના કેન્દ્ર આગળ મૂકેલો છે. જ્યારે તેને સહેજ બદલવામાં આવે તો બિંદુવત વિદ્યુતભાર $x$ અક્ષ થી અનંત સ્થાને પ્રવેગિત થાય છે. બિંદુવત વિદ્યુતભારની એકાંતરીય ઝડપ ....... છે.View Solution
- 4પ્રત્યેક $N$ સૂક્ષ્મ ટીપાંની ત્રિજ્યા $r$ છે. જેને $V$ સ્થિતિમાનથી વિદ્યુતભારીત કરેલ છે. હવે ટીપાંઓ ભેગા મળીને મોટું ટીપું બનાવે છે. તો મોટા ટીપાંનો વિદ્યુતભાર શોધો.View Solution
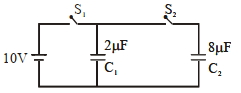
- 5$2\, \mu F$ વાળા $C _{1}$ કેપેસીટરને $10\, V$ ની બેટરી વડે ચાર્જ કરવામાં આવે છે. ત્યારબાદ બેટરી દૂર કરીને $8\, \mu F$ વાળા $C _{2}$ કેપેસીટરને $C _{1}$ સાથે જોડવામાં આવે છે. તો સંતુલન સમયે $C _{2}$ કેપેસીટર પરનો વિદ્યુતભાર ............ $\mu C$ હશે?View Solution
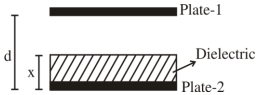
- 6$A$ પ્લેટના ક્ષેત્રફળ તથા $d$ તકતી વચ્યેનું અલગીકરણ દર્શાવતા એક સમાંતર તકતી વાળા સંગ્રાહકમાં $K=4$ પરાવિદ્યુતાંક ધરાવતા પરાવિદ્યુત વસ્તુ ભરેલી છે. પરાવિદ્યુત વસ્તુની જાડાઈ $x$ છે, જ્યા $x < d$.View Solution
ધારો કે $C _1$ અને $C _2$ એ તંત્રની સંગ્રાહકતા $x=\frac{1}{3} d$ અને $x=\frac{2 d}{3}$ માટે અનુક્રમે છે. જો $C _1=2 \mu F$ તો $C _2$ કિમત $........\mu F$ છે.
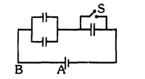
- 7આકૃતિમાં દર્શાવેલ દરેક કેપેસિટર પાસે $5.0\ \mu F$ કેપેસિટન્સ છે. બેટરીનું $emf \,50\ V$ છે. જો $S$ સ્વિચને બંધ કરવામાં આવે તો $AB$ માંથી કેટલો વિદ્યુતભાર વહન પામશે ?View Solution
- 8હવા માધ્યમ ધરાવતા એક સમાંતર બાજુ કેપેસીટરનો કેપેસીટન્સ $6\, \mu F$. છે એક ડાયઈલેક્ટ્રિક માધ્યમ ઉમેરતા આ કેપેસીટન્સ $30\, \mu F$ થાય છે આ માધ્યમની પરમિટિવિટી .......... $C ^{2} N ^{-1} m ^{-2}$ થાયView Solution
$\left(\varepsilon_{0}=8.85 \times 10^{-12} C ^{2} N ^{-1} m ^{-2}\right)$
- 9બે કેપેસીટરોમાંથી એકને ચાર્જ કરેલ નથી અને તેમાં $K$ અચળાંક ધરાવતો ડાઈઈલેક્ટ્રીક ભરેલ છે. જ્યારે અન્ય કેપેસીટરને $V$ જેટલાં સ્થિતિમાને ચાર્જ કરેલ છે તેની પ્લેટો વચ્ચે હવા રહેલ છે. આ બંને કેપેસીટરોને સમાન છેડાઓ વડે જોડવામાં આવે તો તેમનાં સામાન્ય અસરકારક સ્થિતિમાન કેટલો હશે?View Solution
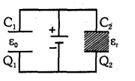
- 10$C_1$ અને $C_2$ બેટરી સાથે જોડેલા છે. $C_1$ ની પ્લેટો વચ્ચેની જગ્યાને હવાથી ભરવામાં આવે છે અને $C_2$ ની પ્લેટો વચ્ચેની જગ્યાને અવાહક વડે ભરવામાં આવે તો...View Solution