ડાઈપોલ મોમેન્ટ $\vec P$ ધરાવતો ડાઈપોલ સમાન વિદ્યુતક્ષેત્રમાં $\vec P$ એ $\vec E$ ને સમાંતર રહે તેમ મુકેલ છે. ડાઈપોલના કેન્દ્રમાંથી પસાર થતી અને $\vec E$ અને $\vec P$ સમાવતા સમતલને લંબ અક્ષને અનુલક્ષીને મુક્ત ફેરવતા થતાં દોલનોનો આવર્તકાળ કેટલો થાય? ડાઈપોલની જડત્વની ચાકમાત્રા $I$ છે.
Medium
b
The dipole experiences a torque \(pE\) \(\sin \theta\) tending to bring itself back in the direction of field.
The dipole experiences a torque \(pE\) \(\sin \theta\) tending to bring itself back in the direction of field.
Therefore, on being released (i.e. rotated) the dipole oscillates about an axis through its centre of mass and perpendicular to the field. If \(I\) is the moment of inertia of the dipole about the axis of rotation, then the equation of motion is
\(I\) \(\mathrm{d}^{2} \theta / \mathrm{dt}^{2}=-\mathrm{pE}\, \sin \theta\)
For small amplitude \(\sin \theta \approx \theta\)
Thus \(\mathrm{d}^{2} \theta / \mathrm{dt}^{2}=-(\mathrm{pE} / \mathrm{I}) \cdot \theta=-\omega^{2} \theta\)
where \(\omega=\sqrt{(\mathrm{pE} / \mathrm{I})}\)
This is a \(S.H.M.\), whose period of oscillation is
\(\mathrm{T}=2 \pi / \omega=2 \pi \sqrt{(\mathrm{I} / \mathrm{pE})}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionવિદ્યુત ડાઈપોલની વિષુવ રેખા પરના એક બિંદુ માટે વિદ્યુતક્ષેત્રની તીવ્રતાની દિશા ....... છે.
- 2અવકાશમાં વિદ્યુતક્ષેત્ર $\overrightarrow E = {E_0}\hat i + 2{E_0}\hat j$ મુજબ આપવામાં આવે છે જ્યાં $E_0\, = 100\, N/C$ છે. $Y-Z$ સમતલને સમાંતર રહેલી $0.02\, m$ ત્રિજ્યા ધરાવતી વર્તુળાકાર સપાટીમાંથી પસાર થતું ફ્લક્સ કેટલું હશે?View Solution
- 3$10\,cm$ બાજુવાળા સમબાજુ ત્રિકોણ $ABC$ ના શિરોબિંદુ પર અનુક્રમે $1\,\mu C$ , $-1\,\mu C$ અને $2\,\mu C$ વિદ્યુતભાર મૂકતાં $C$ પર રહેલ વિદ્યુતભાર પર કેટલા .....$N$ બળ લાગે?View Solution
- 4આકૃતિમાં બતાવેલ બે અનંત પાતળા સમતલની પૃષ્ઠ વિદ્યુતભાર ઘનતા $\sigma$ છે. તો ત્રણ જુદા જુદા પ્રદેશ $E_{ I }, E_{ II }$ અને $E_{III}$ માં વિદ્યુતક્ષેત્ર કેટલું મળે?View Solution
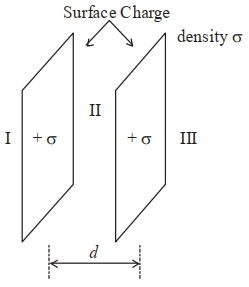
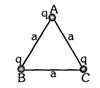
- 5આકૃતિમાં $A$ આગળના વિદ્યુતભાર પરનું બળ $BC$ ને લંબ દિશામાં ...... હશે.View Solution
- 6View Solutionઇલેક્ટ્રીક ડાઈપોલને અસમાન વિધુતક્ષેત્રમાં મુક્તા તે .............. અનુભવે છે
- 7બે સમાન સૂક્ષ્મ (નાના) ગોળા પર $Q_1$ અને $Q_2$ વિદ્યુતભાર ($Q_1$ $>>$ $Q_2$)આવેલ છે. એકબીજા વચ્ચે લાગતું બળ $F_1$ છે. ગોળાને એકબીજા સાથે સંપર્કમાં લઈને તેટલા જ અંતરે રાખવામાં આવે છે. હવે તેમના વચ્ચે લાગતું બળ $F_2$ છે. તો $F_1/F_2$ ...... હશે.View Solution
- 8રેખીય વિદ્યતભાર ઘનતા $\lambda$ ધરાવતી $R$ ત્રિજયાની અર્ધવર્તુળાકાર રીંગના કેન્દ્ર પર વિદ્યુતક્ષેત્ર કેટલું થાય? $\left( {k = \frac{1}{{4\pi {\varepsilon _0}}}} \right)$View Solution
- 9View Solutionકુલંબના નિયમ પ્રમાણે નીચેની આકૃતિ માટે શું સાયું છે ?

- 10વિદ્યુતભાર $Q$ એ ચોરસનાં બે વિરુદ્ઘ શિરોબિંદુઓ પર મૂકેલો છે.બાકીનાં બે શિરોબિંદુઓ પર $-q$ જેટલો વિદ્યુતભાર છે.જો વિદ્યુતભાર $Q$ પર લાગતુ પરિણામી બળ શૂન્ય હોય,તો $\frac{Q}{q}$= ______View Solution
