Frequency of \(1\) st harmonic of \(AB\)
\(=\frac{1}{2 \ell} \sqrt{\frac{\mathrm{T}_{\mathrm{AB}}}{\mathrm{m}}}\)
Frequency of \(2\) nd harmonic of \(\mathrm{CD}\)
\(=\frac{1}{\ell} \sqrt{\frac{\mathrm{T}_{\mathrm{CD}}}{\mathrm{m}}}\)
Given that the two frequencies are equal.
\(\therefore \frac{1}{2 \ell} \sqrt{\frac{\mathrm{T}_{\mathrm{AB}}}{\mathrm{m}}}=\frac{1}{\ell} \sqrt{\frac{\mathrm{T}_{\mathrm{CD}}}{\mathrm{m}}}\)
\(\Rightarrow \frac{\mathrm{T}_{\mathrm{AB}}}{4}=\mathrm{T}_{\mathrm{CD}} \Rightarrow \mathrm{T}_{\mathrm{AB}}=4 \mathrm{T}_{\mathrm{CD}}\) \(...(i)\)
For rotational equilibrium of massless rod, taking torque about point \(O.\)
\(\mathrm{T}_{\mathrm{AB}} \times \mathrm{x}=\mathrm{T}_{\mathrm{CD}}(\mathrm{L}-\mathrm{x})\) \(...(ii)\)
For translational equilibrium,
\(\mathrm{T}_{\mathrm{AB}}+\mathrm{T}_{\mathrm{CD}}=\mathrm{mg}\) \(..(iii)\)
On solving, \((i)\) \(\&(iii)\) we get, \(\mathrm{T}_{\mathrm{CD}}-\frac{\mathrm{mg}}{5}\)
\(\therefore \mathrm{T}_{\mathrm{AB}}=\frac{4 \mathrm{mg}}{5}\)
Substituting these values in \((ii)\) we get
\(\frac{4 m g}{5} \times x=\frac{m g}{5}(L-x)\)
\(\Rightarrow 4 \mathrm{x}=\mathrm{L}-\mathrm{x} \Rightarrow \mathrm{x}=\frac{\mathrm{L}}{5}\)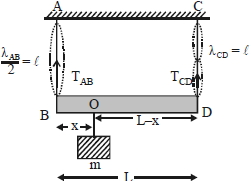
Download our appand get started for free
Similar Questions
- 1$ y = a\cos (kx - \omega \,t) $ તરંગ સાથે બીજા તરંગનું સંપાતીકરણ કરવાથી સ્થિર તરંગ મળે છે.જો $x=0$ પાસે, નિસ્પંદ બિંદુ હોય,તો બીજા તરંગનું સમીકરણ શું હોય?View Solution
- 2બે તરંગોનું સમીકરણView Solution
$y_1=5 \sin 2 \pi(75 t-0.25 x)$
$y_2=10 \sin 2 \pi(150 t-0.50 x)$
છે. આ બે તરંગોની તીવ્રતાનો ગુણોત્તર $\frac{I_1}{I_2}$ કેટલો છે.
- 3$60$ $cm$ લંબાઇ ધરાવતો એક ગેનાઇટનો સળિયો તેનાં મધ્યબિંદુ આગળથી જડિત કરી તેમાં સંગત $(loggitudinal )$ દોલનો પ્રસ્થાપિત કરવામાં આવે છે.ગ્રેનાઇટની ઘનતા $2.7 \times 10^3 $ $kg/m^3$ અને તેનો યંગ મોડયુલસ $9.27 \times 10^{10}$ $Pa$ છે.આ સંગત તરંગોની મૂળભૂત આવૃત્તિ કેટલી ... $kHz$ હશે?View Solution
- 4$3$ અને $5 \,m $ કંપવિસ્તાર ધરાવતા બે તરંગોથી સ્પંદ ઉત્પન્ન કરવામાં આવે છે.મહત્તમ અને લઘુત્તમ તીવ્રતાનો ગુણોત્તર કેટલો થાય?View Solution
- 5જ્યારે બે સ્વરકાંટાને (સ્વરકાંટા$-1$ અને સ્વરકાંટા$-2$) એકસાથે ધ્વનિત કરતાં પ્રતિ સેકન્ડે $4$ સ્પંદ સંભળાય છે. સ્વરકાંટા$-2$ ના પાંખિયા પર ટેપ લગાવવામાં આવે તો પ્રતિ સેકન્ડે $6$ સ્પંદ સંભળાય છે. જો સ્વરકાંટા$-1$ ની આવૃતિ $200\, Hz$ હોય તો સ્વરકાંટા$-2$ ની મૂળભૂત આવૃતિ($Hz$ માં) કટલી હશે?View Solution
- 6પરસ્પર લંબ હોય, તેવા બે રોડ પર $72km/hr$ અને $36 km/hr$ ના વેગથી જતી કાર એકબીજાને ક્રોસ કરે છે,પહેલી કાર $280Hz$ નો હોર્ન વગાડતાં બંને કારને જોડતી રેખાએ રોડ સાથે બનાવેલો ખૂણો $45°$ હોય,તો બીજા કારના ડ્રાઇવરને કેટલી .... $Hz$ આવૃત્તિ સંભળાય?View Solution
- 7સ્વરકાંટો $1sec$ માં $256$ કંપન કરે છે,હવામાં ધ્વનિની ઝડપ $330 \,m/s$ હોય,તો ધ્વનિની તરંગલંબાઇ કેટલી .... $m$ થાય?View Solution
- 8તરંગની આવૃત્તિ‘ $ n $ ’, તરંગલંબાઇ ‘ $ \lambda $ ’અને ઝડપ ‘ $ v $ ’ વચ્ચેનો સંબંધ શું થાય?View Solution
- 9પ્રગામી તરંગનું સમીકરણ $y = 0.02\,\sin \,2\pi \left[ {\frac{t}{{0.01}} - \frac{x}{{0.30}}} \right]$ મુજબ આપવામાં આવે છે. જ્યાં $x$ અને $y$ મીટરમાં અને $t$ સેકન્ડમાં છે. તો તરંગનો વેગ ($ms^{-1}$ માં) કેટલો હશે?View Solution
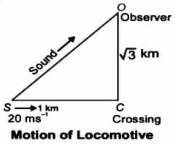
- 10ક્રોસિંગ નજીક પહોંચતી ટ્રેનની ઝડ૫ $20 \,ms ^{-1}$ છે. તે જ્યારે ક્રોસિંગથી $1 \,km$ દુર હોય ત્યારે $640 \,Hz$ આવૃતિની સીટી વગાડે છે. હવા શાંત છે અને હવામાં અવાજની ઝડપ $330\,ms ^{-1}$ છે. ક્રોસિંગથી લંબ રીતે $\sqrt{3} \,km$ દૂર ઉભેલા શ્રોતા વડે ........ $Hz$ આવૃતિ સંભળાશે.View Solution