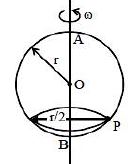
એક $2\pi r$ લંબાઈના તારને વાળીને એક વર્તુળ બનાવીને શિરોલંબ સમતલમાં મૂકવામાં આવે છે એક મણકો તાર પર સરળતાથી સરકી શકે છે જ્યારે વર્તુળને આકૃતિમાં દર્શાવ્યા મુજબ $AB$ની સાપેક્ષે $\omega$ જેટલી કોણીય ઝડપથી ફેરવતા મણકો વર્તુળની સાપેક્ષે $P$ બિંદુ પાસે સ્થિર થાય છે તો $\omega^2$ નું મૂલ્ય કેટલું હશે?

JEE MAIN 2019, Diffcult
d
\(\begin{array}{l}
N\,\sin \,\theta = m\frac{r}{2}{\omega ^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\\
N\,\cos \,\,\theta = mg\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)\\
\tan \,\,\theta \, - \frac{{r{\omega ^2}}}{{2g}}\\
\frac{r}{{2\frac{{\sqrt 3 \,r}}{2}}} = \frac{{r{\omega ^2}}}{{2g}}\,\,\,;\,\,{\omega ^2} = \frac{{2g}}{{\sqrt 3 \,r}}
\end{array}\)
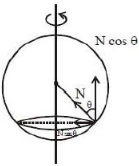
\(\begin{array}{l}
N\,\sin \,\theta = m\frac{r}{2}{\omega ^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\\
N\,\cos \,\,\theta = mg\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)\\
\tan \,\,\theta \, - \frac{{r{\omega ^2}}}{{2g}}\\
\frac{r}{{2\frac{{\sqrt 3 \,r}}{2}}} = \frac{{r{\omega ^2}}}{{2g}}\,\,\,;\,\,{\omega ^2} = \frac{{2g}}{{\sqrt 3 \,r}}
\end{array}\)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક ગાડી અચળ ઝડ૫ સાથે $R_1$ ત્રિજ્યા ધરાવતા વર્તુળાકાર પથ પર ફરે છે. બીજી ગાડી અચળ ઝડ૫ સાથે $R_2$ ત્રિજ્યા ધરાવતા વર્તુળાકાર પથ પર ફરે છે. જો તે બન્નેને એક રાઉન્ડ પૂર્ણ કરવાં માટે સરખો સમય લાગે તો તેની કોણીય ઝડપ અને રેખીય ઝડપનો ગુણોતર અનુક્રમે કેટલો થાય ?View Solution
- 2${m}$ દળના કણને $L$ લંબાઇની દોર વધે બાંધીને છત સાથે લટાવેલ છે. જો કણ ${r}=\frac{{L}}{\sqrt{2}}$ ત્રિજયાના સમક્ષિતિજ વર્તુળાકાર પથ પર ગતિ કરે તો કણની ઝડપ કેટલી હશે?View Solution
- 3નદી $2\,km/h$ ની ઝડપે વહે છે. તરવૈયો $4\,km/h$ ની ઝડપથી તરી શકે છે. નદીને સીધી પાર કરવા માટે નદીના પ્રવાહની સાપેક્ષે તરવૈયાની દિશા ($^o$ માં) શું હોવી જોઈએ?View Solution
- 4$15^o$ ના ખૂણે $u$ વેગથી ફેંકેલા પદાર્થની અવધિ $R$ છે.તો તે પદાર્થને $45^o$ ના ખૂણે $2u$ વેગથી ફેંકતા પદાર્થની અવધિ કેટલી મળે?View Solution
- 5જમીન પર રહેલા માણસને ફૂડ પેકેટ આપવા માટે એક હેલિકોપ્ટર $h$ ઊંચાઈએ સમક્ષિતિજ દિશામાં $v$ વેગથી ગતિ કરે છે.જ્યારે ફૂડ પેકેટ મૂકવામાં આવે હેલિકોપ્ટર માણસથી કેટલા અંતરે હોવું જોઈએ?View Solution
- 6View Solutionટાવર પરથી સમક્ષિતિજ ફેંકેલા પદાર્થ માટે ઊંચાઇ વિરુધ્ધ સમયનો આલેખ કેવો મળે?
- 7એક કણ $25\, cm$ ત્રિજ્યા વાળા એક વર્તુળમાં $2$ ભ્રમણ/સેકન્ડ ના દરે ગતિ કરે છે. તો કણનો $meter/second^2$ માં પ્રવેગ કેટલો થાય?View Solution
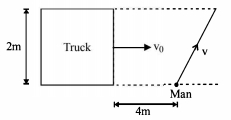
- 8$2\,m$ પહોળાઈનો ટ્રક સીધા આડા રસ્તા પર $v _0=8\,m / s$ ના નિયમિત વેગથી ગતિ કરે છે. એક રાહધરી $v$ જેટલા નિયમિત વેગ થી રોડ ક્રોસ કરે છે જ્યારે ટ્રક તેનાથી $4\,m$ દૂર હોય છે. તે સુરક્ષિત રીતે રોડ ક્રોસ કરે તે માટે $v$ ની ન્યુનત કિંમત $...........\frac{m}{s}$View Solution
- 9સમક્ષિતિજ સાથે $40^{\circ}$ અને $50^{\circ}$ ના ખૂણે અનુકમે બે પ્રક્ષેપણ $A$ અને $B$ કરવામાં આવે છે. જેમનો વેગ સમાન છે.પછી $.............$View Solution
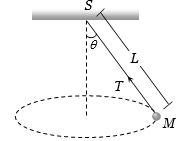
- 10આકૃતિમાં $M$ દળનો પદાર્થ $2/\pi $ પરિભ્રમણ$/sec$ ની કોણીય ઝડપથી ભ્રમણ કરે છે,તો દોરીમાં કેટલો તણાવ ઉત્પન્ન થશે?View Solution