એક આલ્કેન $ 5\,L$ ની સંપૂર્ણ દહન માટે $25\,L$ ઓક્સિજનની જરૂર પડે છે. જો બધા જ કદ અયળ તાપમાને અને દબાણે માપવામાં આવ્યા હોય તો તે આલ્કેન જણાવો.
JEE MAIN 2016, Diffcult
Download our app for free and get started
d
Since the compound undergoing combustion is an alkane. Hence the combustion reaction can be written as
Since the compound undergoing combustion is an alkane. Hence the combustion reaction can be written as
\(\underset{5L}{\mathop{{{C}_{n}}{{H}_{2n+2}}}}\,+\underset{25L}{\mathop{\left( \frac{3n+1}{2} \right){{O}_{2}}}}\,\to \) \(nC{{O}_{2}}+(n+1){{H}_{2}}O\)
since volumes are measured at constant \(T\) & \(P\). Hence according to Avogadro's law
Volume \(\propto \) mole
\(\therefore \,{{n}_{alkane}}=\left( \frac{2}{3n+1} \right)\times {{n}_{{{O}_{2}}}}\)
\(5 = \frac{2}{{3n + 1}} \times 25\)
\(\therefore \,n = 3\)
Hence alkane is propane \((C_3H_8)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionક્યા પ્રક્રિયકોની શ્રેણી દ્વારા એસિટિલિનનું ઉચ્ચ આલ્કાઇનમાં રૂપાંતર કરી શકાય છે ?
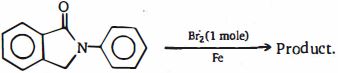
- 2View Solutionપ્રકિયા ની મુખ્ય નીપજ કઈ છે ?
- 3View Solutionનીચે આપેલ પ્રક્રિયામાં બનતી નીપજ શોધો.
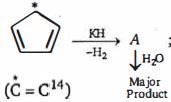
- 4એક ક્લોરો સંયોજન $"A"$View Solution
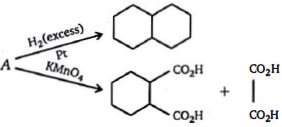
$(i)$ ઓઝોનોલિસિસ પર આલ્ડિહાઈડ્સ બનાવે છે, ત્યારબાદ જલીયકરણ થાય છે.
$(ii)$ જ્યારે ${A}$નું $1.53\, {~g}$ સંપૂર્ણપણે બાષ્પીભવન થાય છે,$STP$ પર $448\, {~mL}$ બાષ્પ આપે છે.
સંયોજન $A$ના પરમાણુમાં કાર્બન અણુઓની સંખ્યા ...... છે.
- 5સંયોજન $(X)$એ ..........View Solution
સંયોજન $(X)$ $\xrightarrow[{Pt}]{{5{H_2}}}$
સંયોજન $(X)$ $\xrightarrow{{AgN{O_3}}}$ અવક્ષેપિત
સંયોજન $(X)$ $\xrightarrow[{M{e_2}S}]{{{O_3}}}$ $\begin{array}{*{20}{c}}
{\,\,\,\,\,\,\,O\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,O\,\,\,\,\,\,\,\,\,\,O\,\,\,\,} \\
{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,||\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,||\,\,\,\,\,\,\,\,\,\,||\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \\
{H - C - C{H_2} - C{H_2} - C - C - H}
\end{array}$ $\begin{array}{*{20}{c}}
{\,\,O\,\,\,\,\,\,O\,\,\,\,\,\,\,\,\,\,} \\
{||\,\,\,\,\,\,\,\,||\,\,\,\,\,\,\,\,\,} \\
{H - C - C - O - H}
\end{array}$ $ + \begin{array}{*{20}{c}}
{O\,\,\,\,\,\,\,} \\
{||\,\,\,\,\,\,\,\,} \\
{H - C - O - H}
\end{array}$ $ + \begin{array}{*{20}{c}}
{CHO} \\
{|\,\,\,\,\,\,\,\,} \\
{CHO}
\end{array}$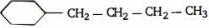
- 6ઇથાઇલ બેન્ઝિનના $KMnO_4$ વડે ઓક્સિડેશનથી કઇ નીપજ મળે છે ?View Solution
- 7સંયોજન $(A)$ શું હશે ?View Solution
- 8નીચેની પ્રક્રિયાની મુખ્ય નીપજ કઈ છે ?View Solution
$\begin{array}{*{20}{c}}
{C{H_3}\,\,\,\,\,\,\,} \\
{|\,\,\,\,\,\,\,\,\,\,\,\,\,} \\
{{H_3}C - C - CH = C{H_2}} \\
{|\,\,\,\,\,\,\,\,\,\,\,\,\,} \\
{C{H_3}\,\,\,\,\,\,\,\,\,}
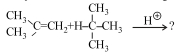
\end{array}$ $\xrightarrow{{{H_2}O/{H^ \oplus }}}{\mkern 1mu} \mathop A\limits_{Major\,product} \, + \,\mathop B\limits_{Minor\,product} $ - 9નીપજ $(C)$ શું હશે ?View Solution
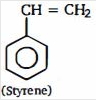
(figure) $\xrightarrow[CC{{l}_{4}}]{B{{r}_{2}}}(A)\xrightarrow[(ii)\,NaN{{H}_{2}}]{(i)\,alc.\,KOH}(B)\xrightarrow[(ii)\,C{{H}_{3}}-Cl]{(i)\,NaN{{H}_{2}}}(C)$
- 10View Solutionનીચે આપેલી પ્રકિયા માં મુખ્ય નીપજ બને છે કઈ છે ?
