(c)
For upstream, Speed \(\Rightarrow v-u\)
(where \(v \rightarrow\) man and \(u \rightarrow\) water)
For downstream, Speed \(\Rightarrow v+u\)
\(t_{ up }=\frac{d}{v-u}\)
\(t_2=\frac{d}{v-u}\)
\(\Rightarrow d=(v-u) t_2 \ldots (i)\)
\(t_{ up }=\frac{d}{v-u}\)
\(t_2=\frac{d}{v-u}\)
\(\Rightarrow d=(v-u) t_2 \ldots (ii)\)
\(t_{ still }=\frac{d}{v}\)
\(t_{\text {still }}=\frac{2 t_1 t_2}{t_1+t_2}\)
On equating \((i)\) and \((ii)\)
\((v-u) t_2=(v+u) t_1\)
\(\Rightarrow v t_2-u t_2=v t_1+u t_1\)
\(\Rightarrow v\left(t_2-t_1\right)=u\left(t_1+t_2\right)\)
\(\Rightarrow u=\frac{v\left(t_2-t_1\right)}{t_2+t_1}\)
So, \(d=\left(v-\frac{v\left(t_2-t_1\right)}{t_1+t_2}\right) t_2=v t_2\left(\frac{t_1+t_2-t_2+t_1}{t_1+t_2}\right)\)
\(\frac{d}{v}=\frac{2 t_1 t_2}{t_1+t_2} \rightarrow\) Remember as shortcut
Download our appand get started for free
Similar Questions
- 1View Solutionનીચે આપેલ વિધાન માંથી ક્યા વિધાન પ્રક્ષેપિત પદાર્થની ગતિ માટે સાચા નથી?
- 2$m$ દળના પદાર્થને l લંબાઇની દોરી વડે બાંઘીને શિરોલંબ સમતલમાં ફેરવતા નીચેના બિંદુ અને ઉપરના બિંદુએ તણાવનો તફાવત કેટલો થાય?View Solution
- 3એક દોલકને પ્રારંભિક $\omega$ $rpm$ જેટલી ઝડપ સાથે સમક્ષિતિજ સમતલમાં દોરી વરે ભ્રમણ કરાવવામાં આવે છે. દોરીમાં $T$ જેટલો તણાવ છે. ત્રિજ્યા સમાન રાખીને જો ઝડપ $2 \omega$ કરવામાં આવે તો દોરીમાં તણાવ. . . . . થશે.View Solution
- 4$x$-અક્ષની સાપેક્ષે ગતિ કરી રહેલ કણોની સ્થિતિ $x=\left(-2 t^3\right.$ $\left.+3 t^2+5\right) \,m$ દ્વારા આપવામાં આવે છે. જે ક્ષણે કણનો વેગ શૂન્ય બને છે ત્યારે કણનો પ્રવેગ ........... $m / s ^2$ થાય?View Solution
- 5કણને $O$ બિંદુથી $u$ વેગથી સમક્ષિતીજ સાથે $\alpha$ ખૂણે ફેકવામા આવે છે જો તે $P$ બિંદુ પાસે તેના વેગની દિશા શરૂઆતની વેગની દિશાને લંબ હોય તો $O$ થી $P$ બિંદુ સુઘી પહોંચતા કેટલો સમય લાગે?View Solution
- 6View Solutionવર્તુળમય ગતિ કરતો કણ સમાન સમયમાં સમાન કોણીય સ્થાનાંતર કરે છે,તો તેનો વેગ સદિશ...
- 7એક બોલને સમાન વેગ $u$ અને સમાન બિંદુથી જુદા જુદા ખૂણા પર ફેંકવામાં આવે છે. તે બંને કિસ્સાઓમાં સમાન અવધિ મળે છે. જો $y_1$ અને $y_2$ એ બે કિસ્સાઓમાં પ્રાપ્ત કરેલી ઊંચાઈ હોય, તો $y_1+y_2=$View Solution
- 8એક વિમાન $1960 \,m$ ઊંચાઇ પર $360 \,km/hr$ ના સમક્ષિતિજ વેગથી ઉડી રહ્યું છે. $A$ બિંદુની બરાબર ઉપર વિમાન હોય ત્યારે,તેમાંથી પદાર્થને પડતો મૂકતા જમીન પર આવતા કેટલા.........$sec$ નો સમય લાગે?View Solution
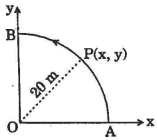
- 9આકૃતિ માં દર્શાવ્યા મુજબ બિંદુ $P$ વિષમઘડી દિશામાં ગતિ કરી રહ્યો છે. બિંદુ $'P'$ $s = t^3+5$ મુજબ ગતિ કરે છે. જ્યાં $s$ મીટરમાં અને $t$ સેકન્ડમાં છે. પથની ત્રિજ્યા $20\;m. $ છે. જ્યારે $t=2$ સેકન્ડ થાય ત્યારે બિંદુ $P$ નો પ્રવેગ.......... $m/s^2$View Solution
- 10પ્રતિપ્ત પદાર્થોના વેગમાં $2 \%$નો વધારો કરતા ઊંચાઈમાં થતો પ્રતિશત વધારો ..... ($\%$ માં)View Solution
