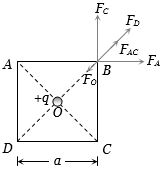
એક ચોરસનાં ચાર શિરોબિંદુઓ પર $-Q$ વિદ્યુતભાર મૂકેલો છે.અને તેના કેન્દ્ર પર $q$ વિદ્યુતભાર મૂકેલો છે. જો તંત્ર સંતુલિત અવસ્થામાં હોય, તો $q$ નું મૂલ્ય કેટલું થાય?
AIEEE 2004, Diffcult
b
(b) If all charges are in equilibrium , system is also in equilibrium.
Charge at centre : charge \(q\) is in equilibrium because no net force acting on it corner charge
If we consider the charge at corner \(B\). This charge will experience following forces
\({F_A} = k\frac{{{Q^2}}}{{{a^2}}},\)\({F_C} = \frac{{k{Q^2}}}{{{a^2}}}\),\({F_D} = \frac{{k{Q^2}}}{{{{(a\sqrt 2 )}^2}}}{\rm{and}}\,{F_O} = \frac{{KQq}}{{{{(a\sqrt 2 )}^2}}}\)
Force at \(B\) away from the centre = \({F_{AC}} + {F_D}\)
\( = \sqrt {F_A^2 + F_C^2} + {F_D} = \sqrt 2 \frac{{k{Q^2}}}{{{a^2}}} + \frac{{k{Q^2}}}{{2{a^2}}} = \frac{{k{Q^2}}}{{{a^2}}}\left( {\sqrt 2 + \frac{1}{2}} \right)\)
Force at \(B\) towards the centre \( = {F_O} = \frac{{2kQq}}{{{a^2}}}\)
For equilibrium of charge at \(B\), \({F_{AC}} + {F_D} = {F_O}\)
\(==>\) \(\frac{{K{Q^2}}}{{{a^2}}}\left( {\sqrt 2 + \frac{1}{2}} \right) = \frac{{2KQq}}{{{a^2}}}\) \(==>\) \(q = \frac{Q}{4}\left( {1 + 2\sqrt 2 } \right)\)
(b) If all charges are in equilibrium , system is also in equilibrium.
Charge at centre : charge \(q\) is in equilibrium because no net force acting on it corner charge
If we consider the charge at corner \(B\). This charge will experience following forces
\({F_A} = k\frac{{{Q^2}}}{{{a^2}}},\)\({F_C} = \frac{{k{Q^2}}}{{{a^2}}}\),\({F_D} = \frac{{k{Q^2}}}{{{{(a\sqrt 2 )}^2}}}{\rm{and}}\,{F_O} = \frac{{KQq}}{{{{(a\sqrt 2 )}^2}}}\)
Force at \(B\) away from the centre = \({F_{AC}} + {F_D}\)
\( = \sqrt {F_A^2 + F_C^2} + {F_D} = \sqrt 2 \frac{{k{Q^2}}}{{{a^2}}} + \frac{{k{Q^2}}}{{2{a^2}}} = \frac{{k{Q^2}}}{{{a^2}}}\left( {\sqrt 2 + \frac{1}{2}} \right)\)
Force at \(B\) towards the centre \( = {F_O} = \frac{{2kQq}}{{{a^2}}}\)
For equilibrium of charge at \(B\), \({F_{AC}} + {F_D} = {F_O}\)
\(==>\) \(\frac{{K{Q^2}}}{{{a^2}}}\left( {\sqrt 2 + \frac{1}{2}} \right) = \frac{{2KQq}}{{{a^2}}}\) \(==>\) \(q = \frac{Q}{4}\left( {1 + 2\sqrt 2 } \right)\)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1વિધુત દ્રી-ધ્રુવી ને કારણે $P$ બિંદુ આગળ વિધુતક્ષેત્ર $E$ મળે છે સમરેખસ્થ એવા $R$ બિંદુએ વિધુતક્ષેત્ર $\frac{E}{x}$.નું મૂલ્ય. . . . . . હશે:View Solution
- 2બે સમાન દળ અને સમાન વિજભાર ધરાવતા બોલને એક બાજુ જડિત કરેલા $l$ લંબાઇની દોરી સાથે જોડેલ છે. સમતોલન સમયે દરેક દોરી દ્વારા બનતો ખૂણો નાનો હોય તો બંને બોલ વચ્ચેનું અંતર $x$ કોના સમપ્રમાણમાં હશે?View Solution
- 3વિદ્યુતભાર $Q$ અને $-3Q$ અમુક અંતરે મૂકેલા છે,$Q$ પર વિદ્યુતક્ષેત્ર $E$ હોય,તો $-3Q$ પર વિદ્યુતક્ષેત્ર કેટલું થાય?View Solution
- 4બે વિજભાર ધરાવતી પ્લેટ વચ્ચે $\vec E$ જેટલું વિદ્યુતક્ષેત્ર પ્રવર્તે છે. એક વિજભાર ધરાવતો કણ આ પ્લેટની વચ્ચે વિદ્યુતક્ષેત્ર $\vec E$ને લંબ રીતે દાખલ થાય છે. તો તે પ્લેટની વચ્ચે કેવા માર્ગે ગતિ કરશે?View Solution
- 5ગોળા અંદર વિદ્યુતભાર $+ 2 × 10^{-6}\ C, -5 × 10^{-6}\ C, -3 × 10^{-6}\ C, +6 × 10^{-6}\ C$ હોય,તો ગોળામાંથી કેટલું ફલ્કસ પસાર થાય?View Solution
- 6ડાઈપોલ માટે પ્રત્યેક વિદ્યુતભારની કિંમત $10^{-10} \,st\, C$ અને તેમના વચ્ચેનું અંતર $1\,\mathop A\limits^o $ હોય તો તેની ડાઈપોલની ચાકમાત્રા ........ છે.View Solution
- 7$10\,\mu C$ નો બિંદુવત વીજભાર $X-$ અક્ષના ઉગમબિંદુ પર રાખેલ છે. અક્ષ પરના સ્થાને $40\,\mu C$ નો બિંદુવત વીજભાર મૂકવાથી પરિણામી વિદ્યુતક્ષેત્ર $x =2\,cm$ આગળ શૂન્ય બનશે ?View Solution
- 8બે $+\sigma$ પૃષ્ઠ વિજભાર ઘનતા ધરાવતા અનંત સમતલને એક બીજા સાથે $30^{\circ} $ ના ખૂણે મૂકવામાં આવે છે, તો તેમની વચ્ચેના ક્ષેત્રમાં વિદ્યુતક્ષેત્ર કેટલું થાય?View Solution
- 9દરેક $+q$ જેટલો વિદ્યાતભાર ધરાવતા બે નાના ગોળાઓ એક $2a$ લંબાઈની અવાહક દોરીથી જોડેલા છે તો દોરીમાં તણાવબળ કેટલું હશે?View Solution
- 10$500 \,\mu C$ જેટલા વિદ્યુતભારિત પોલા વાહક કવચ ઉપર $562.5 \,N$ બળ લગાડતાં તેની સપાટી પરની વિદ્યુતક્ષેત્રની તીવ્રતા ......$N/C$ છે.View Solution
