Before collision after collision
\(\begin{gathered}
\frac{1}{2}mv_1^2 + \frac{1}{2}mv_2^2 = \frac{3}{2}\left( {\frac{1}{2}mv_0^2} \right) \hfill \\
\Rightarrow \,v_1^2 + v_2^2 = \frac{3}{2}v_0^2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,....\left( i \right) \hfill \\
\end{gathered} \)
From momentum conservation
\(m{v_0} = m\left( {{v_1} + {v_2}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,....\left( {ii} \right)\)
Squarring both sides,
\(\begin{gathered}
{\left( {{v_1} + {v_2}} \right)^2} = v_0^2 \hfill \\
\Rightarrow \,v_1^2 + v_2^2 + 2{v_1}{v_2} = v_0^2 \hfill \\
\,\,\,\,\,\,2{v_1}{v_2} = \frac{{v_0^2}}{2} \hfill \\
{\left( {{v_1} - {v_2}} \right)^2} = v_1^2 + v_2^2 - 2{v_1}{v_2} = \frac{3}{2}v_0^2 + \frac{{v_0^2}}{2} \hfill \\
\end{gathered} \)
Solving we get relative velocity between the two particles
\({v_1} - {v_2} = \sqrt 2 {v_0}\)
Download our appand get started for free
Similar Questions
- 1એક બોટ ને અચળ વેગે ચલાવવા માટે લાગતું જરૂરી બળએ તેની ઝડપના વર્ગના સમપ્રમાણમાં છે. જો $v\; km / h$ ઝડપ ને $4 \;kW$ પાવરની જરૂર હોય, તો $2v\; km / h$ ઝડપ ને ........... $kW$ પાવર જરૂર પડશે ?View Solution
- 2$m$ અને $2m$ દળના બે પદાર્થ અનુક્રમે આદર્શ સ્પ્રિંગ અને સ્પ્રિંગ કે જે સ્પ્રિંગો સંકોચાયેલી સ્થિતિમાં છે તેના બે છેડા જોડાયેલા છે. સ્પ્રિંગની ઊર્જા $60$ જૂલ છે. જો સ્પ્રિંગને મુક્ત અથવા છોડવામાં આવે તો.....View Solution
- 3$M$ દળનો એક કણ $R$ જેટલી નિશ્ચિત ત્રિજ્યા ના વર્તુળાકાર માર્ગ પર એવી રીતે ગતિ કરે છે કે $t$ સમયે કેન્દ્રગામી બળ $n^2Rt^2$ દ્વારા આપી શકાય જ્યાં $n$ એ અચળાંક છે.તો કણ પર લાગતાં બળ દ્વારા તેના પર અપાયેલ પાવર કેટલો હશે?View Solution
- 4View Solutionપદાર્થને ટાવર પરથી મુકત કરતાં પ્રથમ,બીજી અને ત્રીજી સેકન્ડમાં થયેલ કાર્યનો ગુણોત્તર કેટલો થાય ?
- 5$10\,g$ નું વજન ધરાવતો કણ સુરેખ રેખામાં $2 x$ પ્રતિબળ સાથે ગતિ કરે છે, જ્યાં $x$ એ $SI$ એકમમાં સ્થાનાંતર છે. ઉપરના સ્થાનાંતર માટે ગતિઊર્જામાં થતો ધટાડો $\left(\frac{10}{x}\right)^{-n}\,J$ છે. $n$ની કિંમત .......... હશે.View Solution
- 6કોઈ કણ એ $F=3 x^2+2 x-10$ જેટલા બળની અસર હેઠળ $x-$અક્ષ $x=0$ થી $x=1\; m$ સુધી ............. $J$ ગતિ કરે છે.View Solution
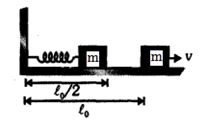
- 7$m$ દળનો એક ટુકડો $k$ સ્પ્રિંગ અચળાંકવાળી એક સ્પ્રિંગ કે જેનો એક છેડો દિવાલ સાથે જોડાયેલ છે તેની વિરૂદ્ધમાં ધકેલાય છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે એક ટુકડો ઘર્ષણરહિત ટેબલ પર સરકે છે. સ્પ્રિંગની પ્રાકૃતિક લંબાઈ $l_0$ છે અને જ્યારે ટુકડો મુક્ત થાય છે ત્યારે તે તેની પ્રાકૃતિક લંબાઈની અડધી લંબાઈ જેટલી સંકોચાય છે તો ટુકડાનો અંતિમ વેગ કેટલો હશે ?View Solution
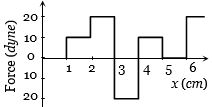
- 8કણનો બળ વિરુધ્ધ સ્થાનનો આલેખ આપેલ છે.તો $ x = 1 cm $ થી $x = 5 cm$ સુધી .......... $ergs$ કાર્ય થશે.View Solution
- 9$40kg$ ના પદાર્થનો વેગ $4m/s$ છે.અને $60kg$ના પદાર્થનો વેગ $2m/s$ છે.બંને વચ્ચે અસ્થિતિસ્થાપક સંધાત થાય,તો ગતિઊર્જામાં થતો ઘટાડો.....$J$View Solution
- 10એક $M$ દળનો પદાર્થ વજનરહિત દોરી વડે લટકાવેલ છે. દોરીને શિરોલંબ સાથે $45^{\circ}$ ના ખૂણે ગોઠવવા માટે પદાર્થ પર કેટલું સમક્ષિતિજ બળ લગાડવું પડે?View Solution
