એક ઘ્વનિ ઉત્પાદક એ $100 \,s^{-1}$ આવૃતિ ઘરાવતા ઘ્વનિ ઉત્પાદક સાથે $5$ સ્પંદ પ્રતિ સેકન્ડ ઉત્પન્ન કરે છે. જો સ્ત્રોતની દ્રિતીય આવૃતિ એ $205\; s^{-1}$ આવૃતિ ઘરાવતા ઘ્વનિ ઉત્પાદક સાથે $5$ સ્પંદ પ્રતિ સેકન્ડ ઉત્પન્ન કરે છે. પ્રથમ ઉત્પાદકની આવૃતિ (${s^{ - 1}}$ માં) કેટલી હશે?
AIPMT 1995, Medium
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$10\;m$ લંબાઇ ધરાવતી દોરીમાં સ્થિત તરંગ ઉત્પન્ન થાય છે. જો દોરી $5$ લૂપમાં કંપન કરે અમે તરંગનો વેગ $20\;m/s$ હોય, તો આવૃત્તિ ($Hz$ માં) કેટલી થશે?View Solution
- 2જ્યારે અવાજનું ઉદગમ સ્થિર શ્રોતા તરફ $V_s$ ઝડપે ગતિ કરે છે ત્યારે તેની આવૃતિમાં $10 \%$ નો વધારો થાય છે. જો ઉદગમ સમાન ઝડપથી શ્રોતાથી દૂર જાય તો આવૃતિમાં ....... $\%$ ટકાનો ફેરફાર થાય. $\left(V_s < V\right)$View Solution
- 3$f$ આવૃત્તિવાળા ઉદ્ગમ સ્થિર અવલોકનકાર તરફ ગતિ કરે છે.તેને સંભળાતી આવૃત્તિ $2f$ હોય,તો ઉદ્ગમનો વેગ કેટલો હશે? હવામાં ધ્વનિનો વેગ $v\, m/s$ છે.View Solution
- 4$380$ અને $384 Hz$ આવૃત્તિ ધરાવતા સ્વરકાંટાને સાાથે કંપન કરાવતા $4$ સ્પંદ ઉત્પન્ન થાય છે. મહત્તમ અવાજ સંભળાયા પછી કેટલા ... $\sec$ સમયે લઘુત્તમ અવાજ સંભળાય?View Solution
- 5$L$ લંબાઈની બંધ ઓર્ગન-પાઈપ અને ખુલ્લી ઓર્ગન-પાઈપમાં અનુક્રમે $\rho_{1}$ અને $\rho_{2}$ ધનતા ધરાવતાં વાયુઓ રહેલા છે. બંને પાઈપોમાં વાયુની દબનીયતા સમાન છે. બંને પાઈપ સમાન આવૃત્તિ સાથે પોતાના પ્રથમ અધિસ્વર (overtone) માં કંપન કરે છે. ખુલ્લા પાઈપની લંબાઈ $\frac{ x }{3} L \sqrt{\frac{\rho_{1}}{\rho_{2}}}$ છે. જ્યાં $x$ ........... છે. (નજીકતમ પૂર્ણાંકમાં લખો)View Solution
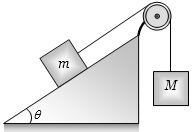
- 6$ 9.8 \times {10^{ - 3}}kg{m^{ - 1}} $ રેખીય દળ ધરાવતા તાર દ્વારા $30^°$ ના ઢાળવાળો ધર્ષણરહિત ઢાળ પર બે પદાર્થ આકૃતિ મુજબ બાંધેલા છે,તંત્ર સંતુલન સ્થિતિમાં હોય,ત્યારે તારમાં લંબગત તરંગની ઝડપ $100 m/s$ હોય, તો દળ $m$ કેટલું $m =$ ..... $kg$ હશે?View Solution
- 7$L$ લંબાઇની કલોઝડ પાઇપ અને $L’$ લંબાઇની ઓપન પાઇપમાં $ {\rho _1} $ અને $ {\rho _2} $ ઘનતા ઘરાવતાા ગેસ ભરેલ છે. બંને ગેસની દબનીયતા સરખી છે. બંને પ્રથમ ઓવરટોન સાથે અનુનાદિત થાય છે.ઓપન પાઇપની લંબાઇ $ L’=$________View Solution
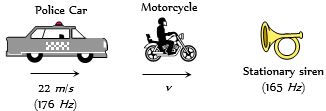
- 8એક બાઇક પાછળ પોલિસની કાર $22 m/s$ ની ઝડપથી જઇ રહી છે.પોલીસની કાર દ્રારા $176 Hz $ આવૃતિ ઘરાવતો હોર્ન વગાડવામાં આવે છે. બંને એક $165 Hz$ ઘરાવતા સાઇરન તરફ ગતિ કરી રહયા છે.જો બાઇક સવારને સ્પંદ અનુભવાતા ન હોય તો બાઇકની ઝડપ ... $m/s$ કેટલી હશે? (હવામાં ઘ્વનિની ઝડપ $330 m/s$ )View Solution
- 9$NTP$ એ રહેલ $4.0\; g$ વાયુ $22.4$ લિટર કદ રોકે છે. અચળ કદે વિશિષ્ટ ઉષ્માધારિતા $5.0\; JK^{-1}mol^{-1}$ છે. જો $NTP$ એ આ વાયુમાં ધ્વનિનો વેગ $952 \;ms^{-1}$ હોય, તો અચળ દબાણે વાયુની વિશિષ્ટ ઉષ્માધારિતા ($J K^{-1} mol^{-1}$) કેટલી થાય?View Solution
(વાયુનો અચળાંક $R=8.3 \;JK ^{-1} mol ^{- 1}$ લો)
- 10એક સ્થિત તરંગમાં પ્રસ્પંદ પરના બિંદુુનો કંપવિસ્તાર $4\,cm$, છે. તો પ્રસ્પંદ અને નિસ્પંદની બરોબર મધ્યમાં આવેલા માધ્યમના કણનો કંપવિસ્તાર .......... $cm$ છે.View Solution