એક જંતુ અર્ધગોળાકાર સપાટી પર ધીમે ધીમે ચડે છે. જંતુ અને સપાટી વચ્ચે નો ઘર્ષણાંક $1/3$ છે.જો જો જંતુ અને અર્ધગોળાકાર સપાટી ના કેન્દ્ર ને જોડતી રેખા શિરોલંબ સાથે $\alpha $ નો ખૂણો બનાવતો હોય તો જંતુ સરકી ન જાય તેના માટે $\alpha $ ની મહત્તમ શક્ય કિંમત શું થાય?


AIEEE 2012,IIT 2001, Diffcult
a
\(\begin{array}{l}
The\,{\rm{insect}}\,crawls\,up\,the\,bowl\,upto\,a\\
certain\,height\,h\,only\,till\,the\,component\\
of\,its\,weight\,along\,the\,bowl\,is\,balanced\,\\
by\,{\rm{limiting}}\,frictional\,force\\
For\,li\,miting\,condition\,at\,{\rm{point}}\,A\\
R = mg\,\cos \alpha \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\\
{F_1} = mg\,\sin \alpha \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)
\end{array}\)
\(\begin{array}{l}
The\,{\rm{insect}}\,crawls\,up\,the\,bowl\,upto\,a\\
certain\,height\,h\,only\,till\,the\,component\\
of\,its\,weight\,along\,the\,bowl\,is\,balanced\,\\
by\,{\rm{limiting}}\,frictional\,force\\
For\,li\,miting\,condition\,at\,{\rm{point}}\,A\\
R = mg\,\cos \alpha \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\\
{F_1} = mg\,\sin \alpha \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)
\end{array}\)
\(\begin{array}{l}
Dividing\,eq.\,\left( {ii} \right)\,by\,\left( i \right)\\
\tan \,\alpha \, = \frac{1}{{\cot \,\alpha }} = \frac{{{F_1}}}{R} = \mu \left[ {As\,{F_1} = \mu R} \right]\\
\Rightarrow \,\tan \alpha \, = \mu = \frac{1}{3}\left[ {\mu = \frac{1}{3}\left( {given} \right)} \right]\\
\therefore \,\,\cot \alpha \, = 3
\end{array}\)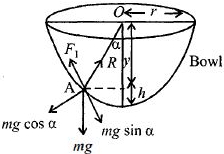
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$10 \,kg$ દળનાં એક બ્લોકને $30^{\circ}$ નો ઢોળાવ ખૂણો ધરાવતી નિશ્વિત ખરબચડી $(\mu=0.8)$ કોણીય સપાટી પર મુકેલ છે. બ્લોક પર લાગતું ઘર્ષણબળ ............ $N$ છે.View Solution
- 2View Solutionજ્યારે સાઇકલ ગતિમાં હોય ત્યારે સપાટી દ્વારા બંને પૈડાં પર લાગતું ઘર્ષણબળ કઈ રીતે કામ કરે ?
- 3રફ સપાટી પર પડેલ $64 \,N$ ના બ્લોકને ગતિ માટે જરૂરી બળ આપવામાં આવે છે.બ્લોક ગતિમાં આવ્યા પછી પણ આ બળ લગાવવાનું શરૂ રાખવામાં આવે,તો તે કેટલો પ્રવેગ પ્રાપ્ત કરશે? બ્લોક અને સપાટી વચ્ચેનો સ્થિત અને ગતિક ઘર્ષણાંક અનુક્રમે $0.6$ અને $0.4$ છેView Solution
- 4દિવાલ સામે સ્થિર બ્લોકને પકડી રાખવા માટે $10 \,N$ નું સમક્ષિતિજ બળ જરૂરી છે. બ્લોક અને દિવાલ વચ્ચેના ઘર્ષણનો ગુણાંક $0.2$ છે. બ્લોકનું વજન ($N$ માં) કેટલું હશે?View Solution
- 5જો કોઈ સાઇકલચાલક $4.9\, m/s$ ની ઝડપે સ્તરીય માર્ગ પર $4 \,m$ ત્રિજ્યાનો વળાંક લઈ શકતો હોય તો સાઇકલ ના ટાયર અને રસ્તા વચ્ચેનો ઘર્ષણાંક કેટલો હશે?View Solution
- 6રફ સપાટી પર પડેલ $64 \,N$ ના બ્લોકને ગતિ માટે જરૂરી બળ આપવામાં આવે છે.બ્લોક ગતિમાં આવ્યા પછી પણ આ બળ લગાવવાનું શરૂ રાખવામાં આવે,તો તે કેટલો પ્રવેગ પ્રાપ્ત કરશે? બ્લોક અને સપાટી વચ્ચેનો સ્થિત અને ગતિક ઘર્ષણાંક અનુક્રમે $0.6$ અને $0.4$ છેView Solution
- 7$4\, kg$ દળ ધરાવતો બ્લોક $A$ ને બીજા $5\, kg$ દળ ધરાવતા બ્લોક $B$ પર મુકેલ છે અને બ્લોક $B$ એ લીસ્સા સમક્ષિતિજ ટેબલ પર પડ્યો છે. જો બંને બ્લોક ને એકસાથે ખસેડવા માટે $A$ પર લગાવવું પડતું ન્યુનત્તમ બળ $12\, N$ છે તો બંને બ્લોક ને સાથે ખસેડવા માટે $B$ પર લગાવવું પડતું મહત્તમ બળ ........ $N$ થાય.View Solution
- 8જો ${\mu _s},\,{\mu _k}$ અને ${\mu _r}$ સ્થિત ઘર્ષણાંક ગતિક ઘર્ષણાંક અને રોલિંગ ઘર્ષણાંક હોય તોView Solution
- 9એક કાર $50\,m$ ત્રિજ્યાવાળા વક્ર અને સમક્ષિતજ રસ્તા પર ગતિ કરે છે. જો ટાયર અને રસ્તા વચ્યેનું ધર્ષણ $0.34$ હોય, તો કારની મહત્તમ ઝડપ $..........\,ms^{-1}$ હશે. $\left[ g =10 ms ^{-2}\right]$View Solution
- 10$30^{\circ}$ સમક્ષિતિજ સાથે ખૂણો ધરાવતા ઢાળ પર ઉપર તરફ $10\, {ms}^{-2}$ ના પ્રવેગથી એક કાર ગતિ કરે છે. કારની છત પર દોરી બાંધી તેના છેડે લોકલ લટકાવેલ છે. તો દોરીએ શિરોલંબ સાથે બનાવેલ ખૂણો કેટલો હશે? (${g}=10\, {ms}^{-2}$ )View Solution
