એક ખેંચ્યા વગર ની સ્પ્રિંગ લંબાઈ $l$ અને દળ $m$ ધરાવે છે અને તેનો એક છેડો દ્રઢ આધાર સાથે જોડેલો છે.ધારો કે સ્પ્રિંગ ને એકસમાન તાર થી બનાવેલી છે તો તેના એક છેડાને સમાન વેગ $v$ થી ખેંચવામાં આવે છે તો તેણે મેળવેલી ગતિઉર્જા કેટલી થશે?
JEE MAIN 2014, Diffcult
d
We can find the effective mass of the spring by finding its kinetic energy. This requires adding all the length elements' kinetic energy, and requires the following integral:
We can find the effective mass of the spring by finding its kinetic energy. This requires adding all the length elements' kinetic energy, and requires the following integral:
\(T=\int_{m} \frac{1}{2} u^{2} d m\)
since the spring is uniform, \(d m=\left(\frac{d y}{L}\right) m,\) where \(L\) is the length of the spring. Hence,
\(T =\int_{0}^{L} \frac{1}{2} u^{2}\left(\frac{d y}{L}\right) m\)
\(=\frac{1}{2} \frac{m}{L} \int_{0}^{L} u^{2} d y\)
The velocity of each mass element of the spring is directly proportional to its length, i.e.
\(u=\frac{v y}{L},\) from which it follows\(:\)
\({T=\frac{1}{2} \frac{m}{L} \int_{0}^{L}\left(\frac{v y}{L}\right)^{2} d y}\)
\({=\frac{1}{2} \frac{m}{L^{3}} v^{2} \int_{0}^{L} y^{2} d y}\)
\({=\frac{1}{2} \frac{m}{L^{3}} v^{2}\left[\frac{y^{3}}{3}\right]_{0}^{L}}\)
\({=\frac{1}{2} \frac{m}{3} v^{2}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જેનો અકડ (ચુસ્ત) અચળાંક $k $ હોય તેવી સ્પ્રિંગના ઉપરના ભાગ પરથી $m$ દળના એક ટુકડાને એકાએક (અચાનક) મુક્ત કરાવવામાં આવે છે. $(i)$ સ્પ્રિંગમાં મહત્તમ સંકોચન કેટલું હશે ? $(ii) $ સંતુલન સ્થિતિએ, સ્પ્રિંગમાં સંકોચન કેટલું હશે ?View Solution
- 2$m$ દળ ધરાવતો એક કણ અયળ ત્રિજ્યા $r$ ધરાવતા વર્તુળાકાર પથ પર એવી રીતે ગતિ કરે છે કે જેથી તેનો કેન્દ્રગામી પ્રવેગ $(a)$ સમય $t$ સાથે $a= k ^{2} r t^{2}$, જ્યા $k$ એ અચળાંક છે, મુજબ બદલાય છે. તેના પર લાગતા બળ દ્વારા અપાતી કાર્યત્વરા (પાવર) ......... મુજબ આપી શકાય.View Solution
- 3$0.5\; kg$ નો પદાર્થ $1.5\; m/s$ ના વેગથી સમક્ષિતિજ લિસી સપાટી પર ગતિ કરીને $50\; N/m$ બળઅચળાંક ધરાવતી દળરહિત સ્પિંગ્ર સાથે અથડાય છે. સ્પિંગનું મહત્તમ સંકોચન ($m$ માં) કેટલું થાય?View Solution
- 4${m}$ દળના પદાર્થને $h$ ઊંચાઈ પરથી મુક્ત કરતાં તે જમીન પર $0.8 \sqrt{{gh}}$ ના વેગ વેગથી પહોચે છે. હવાના ઘર્ષણના કારણે થતું કાર્ય $.....\,{mgh}$ હશે.View Solution
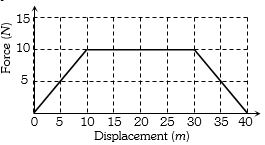
- 5કણનો બળ વિરુધ્ધ સ્થાનનો આલેખ આપેલ છે.તો $ x = 0 m$ થી $x = 35 m $ સુધીમાં કેટલા .......... $J$ કાર્ય થશે?View Solution
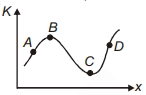
- 6View Solutionએક ચલ બળની અસર હેઠળ ગતિ કરી રહેલ એક કણ માટેનો ગતિઊર્જા - સ્થિતિ(સ્થાન)નો ગ્રાફ આપેલ છે, તો...
- 7બે અનુક્રમે $m$ અને $2\, m$ દળ વાળા પદાર્થો $A$ અને $B$ ને લીસ્સી સપાટી પર મૂકેલા છે. તેઓને અવગણ્ય દળ ધરાવતી સ્પ્રિંગ સાથે જોડેલા છે . ત્રીજો $m$ દળનો પદાર્થ $C$ ને સપાટી પર મૂકેલો છે. પદાર્થ $C$ વેગ $v_0$ થી $A$ અને $B$ ને જોડતી રેખા પર ગતિ કરીને $A$ સાથે સ્થિતિસ્થાપક સંઘાત પામે છે. સંઘાત પછી ચોક્કસ સમય બાદ એવું જોવા મળ્યું કે $A$ અને $B$ નો તત્કાલિન વેગ સમાન છે અને સ્પ્રિંગ નું સંકોચન $x_0$ છે. તો સ્પ્રિંગ અચળાંક $k$ કેટલો થશે?View Solution
- 8View Solutionજ્યારે બે કણો અથડાય છે ત્યારે સામાન્ય રીતે શું સાચું હશે?
- 9$10 cm$ લંબાઈની એક હલકી સ્પ્રિંગના છેડે જ્યારે $20 g$ દળનો પદાર્થ જોડેલો હોય ત્યારે સ્પ્રિંગ $2 cm$ જેટલી ખેંચાય છે. સ્પ્રિંગની કુલ લંબાઈ $4 cm$ થાય ત્યાં સુધી પદાર્થને લટકાવવામાં આવેલ છે. સ્પ્રિંગમાં સંગ્રહીત સ્થિતિ સ્થાપક ઊર્જા (જૂલમાં) કેટલી હશે ?View Solution
- 10એક $m $ દળનો લીસો ગોળો $u$ વેગથી પૃષ્ઠ (સપાટી) પર ગતિ કરે છે જે તેટલા જ પરીમાણના $2m $ દળના બીજા લીસા ગોળા સાથે અથડાય છે. સંઘાત પછી બીજા ગોળાના વેગની અવધિ કેટલી હશે ?View Solution
