એક લાંબા નળાકારીય કદ ધનતા $\rho$ ધરાવતું નિયમિત વિદ્યુતભાર વિતરણ ધરાવે છે. નળાકારીય કદની ત્રિજ્યા $R$ છે. એક $q$ વિદ્યુતભારીત કણ તેની આસપાસ વર્તુળાકાર પથ પર ભ્રમણ કરે છે. વિદ્યુતભારની ગતિઉર્જા ......થશે.
JEE MAIN 2022, Diffcult
a
\(E\cdot 2 \pi r \ell=\frac{\rho \pi r ^{2} \ell}{\varepsilon_{0}}\)
\(E\cdot 2 \pi r \ell=\frac{\rho \pi r ^{2} \ell}{\varepsilon_{0}}\)
\(qE =\frac{ q \rho R ^{2}}{2 \varepsilon_{0} r }=\frac{ mv ^{2}}{ r }\)
\(mv ^{2}=\frac{ q \rho R ^{2}}{2 \varepsilon_{0}}\)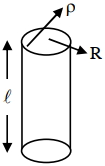
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$\lambda$ વિદ્યુતભાર ઘનતા ધરાવતા બે લાંબા પાતળા વિદ્યુતભારીત સળિયાને એકબીજને સમાંતર $d$ અંતરે મૂકવામાં આવ્યા છે. એક સળીયા બીજા સળીયા પર એકમ લંબાઈ દીઠ લાગતું બળ કેટલું હશે? $\left(\right.$ જ્યાં $\left.k=\frac{1}{4 \pi \varepsilon_0}\right)$View Solution
- 2વિધુત દ્રી-ધ્રુવી ને કારણે $P$ બિંદુ આગળ વિધુતક્ષેત્ર $E$ મળે છે સમરેખસ્થ એવા $R$ બિંદુએ વિધુતક્ષેત્ર $\frac{E}{x}$.નું મૂલ્ય. . . . . . હશે:View Solution
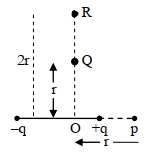
- 3અનુક્રમે, $+ \sigma$ અને $+ \lambda$ વિદ્યુતભાર ધનતા ધરાવતા એક અનંત પૃષ્ઠ વિદ્યુતભાર અને અનંત રેખીય વિદ્યુતભારને, એકબીજાને સમાંતર $5\,m$ અંતરે રાખવામાં આવે છે. બિંદુ $P$ અને $Q$ એ રેખીય વિદ્યુતભારથી લંબઅંતરે પૃષ્ઠ તરફ અનુક્રમે $\frac{3}{\pi}\, m$ અને $\frac{4}{\pi}\,m$ અંતરે રહેલા બિંદુ છે. બિંદ્દુ $P$ અને $Q$ આગળ પરિણામી વિદ્યુતક્ષેત્ર ના મૂલ્યો અનુક્રમે $E_P$ અને $E _Q$ છે. જો $2|\sigma|=|\lambda|$ હોય, તો $\frac{E_P}{E_Q}=\frac{4}{a}$ મળે છે. $a$ નું મૂલ્ય ....... થશે.View Solution
- 4સમાન મૂલ્ય q ધરાવતા બે વિદ્યુતભારો $X-$ અક્ષ પર $ x=-a$ અને $x=a$ આગળ રાખેલ છે. $m$ દળ ધરાવતો અને $q_0=\frac{q}{2}$ વિદ્યુતભાર ધરાવતો એક કણ ઊગમબિંદુ પર મૂકેલ છે.હવે જો $q_0$ વિદ્યુતભારને $Y-$ અક્ષની દિશામાં શૂક્ષ્મ સ્થાનાંતર $(y < < a) $ આપવામાં આવે,તો કણ પર લાગતું પરિણામી બળ _______ ના સમપ્રમાણમાં હશે.View Solution
- 5એક વિસ્તારમાં વિદ્યુતક્ષેત્ર એકરૂપ છે. અને $\vec{E}=a \hat{i}+b \hat{j}+c \hat{k}$ વડે આપવામાં આવેલ છે. $\vec{A}=\pi R^2 \hat{i}$ ક્ષેત્રફળની સપાટી સાથે સંકળાયેલ વિદ્યુત ફલક્સ કેટલું છે?View Solution
- 6ડાઈપોલ મોમેન્ટ $\vec P$ ધરાવતો ડાઈપોલ સમાન વિદ્યુતક્ષેત્રમાં $\vec P$ એ $\vec E$ ને સમાંતર રહે તેમ મુકેલ છે. ડાઈપોલના કેન્દ્રમાંથી પસાર થતી અને $\vec E$ અને $\vec P$ સમાવતા સમતલને લંબ અક્ષને અનુલક્ષીને મુક્ત ફેરવતા થતાં દોલનોનો આવર્તકાળ કેટલો થાય? ડાઈપોલની જડત્વની ચાકમાત્રા $I$ છે.View Solution
- 7મુક્ત અવકાશમાં $z-$અક્ષ પર $8\, nC / m$ ના સમાંગ રેખીય વિદ્યુતભાર ધરાવતાં વિસ્તરમાં $x =3\, m$ બિંદુ આગળ વિદ્યુત ફલક્સ ઘનતા શોધો :View Solution
- 8સામાન્ય બિંદુએ, $l$ લંબાઇની દળરહિત દોરીઓ સાથે બે આદર્શ વિદ્યુતભારિત ગોળાઓ લટકાવ્યા છે.તેમની વચ્ચે લાગતા અપાકર્ષણનાં કારણે શરૂઆતમાં તેમની વચ્ચેનું અંતર $d \,(d << l)$ છે.બંને ગોળામાંથી વિદ્યુતભાર સમાન દરથી લીક થવાનું શરૂ થાય છે અને તેના લીધે ગોળાઓ એકબીજા તરફ $v$ વેગથી નજીક આવે છે ત્યારે ગોળા વચ્ચેનું અંતર $x$ ને વેગ $v$ ના વિધેયને કયા સ્વરૂપે મળશે?View Solution
- 9$25.5\, k\,Vm^{-1}$ જેટલા વિદ્યુતક્ષેત્રમાં $6$ વધારાના ઇલેક્ટ્રોન ધરાવતા પ્રવાહીના ટીપાને સ્થિર રાખવામા આવે છે.પ્રવાહીની ઘનતા $1.26\times10^3\, kg\, m^{-3}$ હોય તો ટીપાની ત્રિજ્યા કેટલી હશે?View Solution
- 10$1$ થી $5$ અંકિત કરેલા પાંચ દડાઓ અલગ-અલગ દોરી વડે લટકાવેલા છે. જોડ $(2, 3)$ અને $(4, 5)$ સ્થિતવિદ્યુત અપાકર્ષણ દર્શાવે છે. જ્યારે જોડ $(1, 2),(3, 5)$ અને $(1, 5)$ સ્થિત વિદ્યુત આકર્ષણ દશાવે છે. $1$ અંકિત દડો કેવો હોવો જોઈએ?View Solution
