Angular momentum will remain the same since external torque is zero.
MI will increase since \(r\) increases \(\left( I =\frac{2}{5} mr ^2\right)\)
Angular velocity decreases since \(L = I \omega\) is conserved.
Rotational KE: \(K _{ rot }=\frac{ L ^2}{2 I }\) decreases since I increases.
Download our appand get started for free
Similar Questions
- 1એક પદાર્થ એક સ્થિર અક્ષને અનુલક્ષીને $3 \,rad / s ^2$ ના કોણીય પ્રવેગ સાથે ભ્રમણ કરે છે. જે સમયે તેનો કોણીય વેગ $10 \,rad / s$ માંથી. વધી ને $20 \,rad / s$ થાય તે સમય દરમિયાન તેના દ્વારા ભ્રમણ કરવામાં આવેલો કોણ ($rad$ માં) શું થાય?View Solution
- 2વ્યાસ પર ગોળાની જડત્વની ચાકમાત્રા $ 40\ kg. m^2$ છે. કોઈ પણ સ્પર્શક પર જડત્વની ચાકમાત્રા શોધો.View Solution
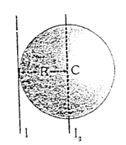
- 3સમાન દળ ' $M$ અને ' $2 R$ ' જેટલી ત્રિજ્યા ધરાવતા ચાર વસ્તુઆની ઝડત્વની ચાકમાત્રા $(M.I.)$ નીચે મુજબ છેView Solution
$I _{1}=$ તેના વ્યાસને અનુલક્ષીને ધન ગોળાની $M.I.$
$I _{2}=$ તેની અક્ષને અનુલક્ષીને ધન નળાકારની $M.I.$
$I _{3}=$ તેના વ્યાસને અનુલક્ષીને ધન તક્તિની $M.I.$
$I _{4}=$ તેના વ્યાસને અનુલક્ષીને પાતળી વર્તુળાકાર રીંગની $M.I.$
જો $2\left( I _{2}+ I _{3}\right)+ I _{4}=x \cdot I _{1}$ હોય તો $x$ નું મૂલ્ય ........થશે.
- 4આ પ્રશ્ન માં વિધાન $1$ અને વિધાન $2$ છે. આપેલ ચાર વિકલ્પોમાથી બંધબેસતો વિકલ્પ પસંદ કરો.View Solution
વિધાન $1$: જો પોતાની અક્ષને અનુલક્ષીને કોણીય ઝડપ $\omega $ થી ભ્રમણ કરતાં પદાર્થની જડત્વની ચાકમાત્રામાં વધારો થાય તો તેના કોણીય વેગ $L$ માં કોઈ પણ ફેરફાર નહિ થાય પણ જો ટોર્ક લગાવેલ નહિ હોય તો ગતિઉર્જા $K$ વધશે.
વિધાન $2$: $L = I\omega $, ભ્રમણ ની ગતિઉર્જા $ = \frac{1}{2}\,I\omega ^2$
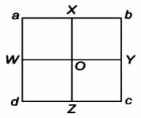
- 5એક સમચોરસ પ્લેટ $abcd$ $1 \,kg$ દળ ધરાવે છે. જો નીચે દર્શાવ્યા પ્રમાણે $b$ અને $c$ ખૂણા પર દરેકનું દળ $20 \,g$ હોય તેવા બે બિંદુ દળો મુક્વામાં આવે તો દ્રવ્યમાન કેન્દ્ર કઈ રેખા પર ખસશે?View Solution
- 6$R$ ત્રિજયાના એકસમાન અર્ધ-વર્તુળાકાર તારને $x-y$ સમતલમાં મૂકવામાં આવેલ છે જેનું કેન્દ્ર ઉગમબિંદુ પર અને તેમના છેડાને જોડતી રેખા $x-$ અક્ષ તરીકે આપવામાં આવે તો તેનું દ્રવ્યમાન $\left(0, \frac{x R}{\pi}\right)$ મુજબ આપવામાં આવે, તો $|x|$ નું મૂલ્ય કેટલું હશે?View Solution
- 7ત્રણ દળ ${m_1},\,{m_2},\,{m_3}$ એક સમબાજુ ત્રિકોણ જેની બાજુની લંબાઈ $a$ છે તેના શિરોબિંદુ પર મૂકેલા છે. તો ત્રિકોણની ઊંચાઈની ની દિશામાં $m_1$ ને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય ?View Solution
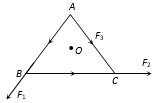
- 8$ABC$ એ સમબાજુ ત્રિકોણ છે, જેનું કેન્દ્ર $O$ છે. $\vec{F}_{1}, \vec{F}_{2}$ અને $\vec{F}_{3}$ એ અનુક્રમે $AB, BC$ અને $AC$ બાજુ પર લાગતાં બળો છે. જો $O$ ને અનુલક્ષીને કુલ ટોર્ક શૂન્ય હોય, તો $\vec{F}_{3}$ નું મૂલ્ય કેટલું હશે?View Solution
- 9View Solutionકેન્દ્રીય બળની અસર હેઠળ કોનું સંરક્ષણ થાય?
- 10નિયમિત વર્તુળાકાર ગતિ કરતા એેક કણ નો કોણીય વેગમાન $L$ છે. જો કણ ની ગતિઊર્જા બમણી કરવામાં આવે અને આવૃત્તિને અડધી કરવામાં આવે તો કોણીય વેગમાન શું બને છે ?View Solution
