એક તારની લંબાઈ $L$ અને આડછેદનું ક્ષેત્રફળ $A$ છે તેની બંને બાજુના છેડા પર $F$ બળ લગાવતા તેની લંબાઈમાં $l$ નો વધારો થાય તો નીચેના માથી શું સાચું છે ?
Easy
Download our app for free and get started
c
(c) \(l = \frac{{FL}}{{YA}} \Rightarrow l \propto \frac{1}{A}\)
(c) \(l = \frac{{FL}}{{YA}} \Rightarrow l \propto \frac{1}{A}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$25\, cm$ લંબાઇ અને $2\,mm$ ત્રિજયા ધરાવતા તાર નો એક છેડા જડિત છે, અને બીજા છેડે ટોર્ક લગાવતાં કોણીય સ્થાનાંતર ${45^o}$ કરવા ......... $J$ કાર્ય કરવું પડે . $(\eta = 8 \times {10^{10}}\,N/{m^2})$View Solution
- 2View Solutionદ્રવ્યના આકાર, કદ અને લંબાઈમાં થતાં ફેરફારનો અવરોધ કરનાર દ્રવ્યના લક્ષણને શું કહે છે ?
- 3જયારે $10$ $cm $ લાંબા સ્ટિલના તારના તાપમાનમાં $100^o $ $C$ નો વધારો કરવામાં આવે,ત્યારે તારની લંબાઇ અચળ રાખવા માટે તેના છેડાઓ પર લગાવવું પડતું દબાણ ( સ્ટિલનો યંગ મોડયુલસ $2 \times 10^{11}$ $Nm^{-1}$ અને તાપીય પ્રસરણાંક $1.1 \times 10^{-5}$ $K^{-1}$ છે.)View Solution
- 4સમાન દ્રવ્યના બનેલા તાર $A$ અને $B$ પર સમાન બળ $2\,N$ લગાવીને તેમની લંબાઈ $2 \,mm$ અને $4\, mm$ વધારવામાં આવે છે.$B$ની ત્રિજ્યા $A$ કરતા ચાર ગણી છે,બંનેની લંબાઇનો ગુણોતર $a / b\,=\,1 / x$ હોય તો $x=\,.......$View Solution
- 5આકૃતિમાં દર્શાવ્યા પ્રમાણે સળીયાને અક્ષના અનુલક્ષમાં બળ આપવામા આવે છે. $E$ એ સ્થિતીસ્થાપકતા અંક છે. $A$ આડછેદનું ક્ષેત્રફળ છે. તો તેમા થતુ વિસ્તરણ .....View Solution
- 6દ્રવ્ય માટે તેની સ્થિતિસ્થાપક હદમાં રેખીય પ્રતિબળ અને રેખીય વિકૃતિનો આલેખ આકૃતિમાં દર્શાવેલ છે. $5 \times 10^{-4}$ જેટલી રેખીય વિકૃતિ માટે ઊર્જા ઘનતામાં થતો વઘારો ............ $kJ / m ^{3}$ હશે.View Solution
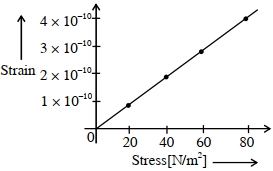
- 7$2 \,m$ લંબાઈ અને $50\,m{m^2}$ આડછેદનું ક્ષેત્રફળ ધરાવતા લોખંડના તાર પર $250\,kg$ નું દળ લગાવતા તેની લંબાઈમાં થતો વધારો $0.5\, mm$ છે તો લોખંડના તારનો યંગ મોડ્યુલસ કેટલો હશે ?View Solution
- 8$Y= 49000 \frac{m}{l} \frac{d y n e}{c^2}$ સૂત્ર વડે યંગ મોડ્યુલસ શોધવામાં આવે છે, જ્યાં પ્રયોગમાં $M$ એ દળ અને $l$ એ તારમાં ઉત્પન ખેંચાણ છે. હવે ગ્રાફ પેપરમાં $M-l$ આલેખ પરથી યંત્ર મોડ્યુલસ ($Y$)માં ત્રૂટિનું અનુમાન લગાવવામાં આવે છે. ભાર-અક્ષ અને ખેંચાણ (extension) -View Solution
અક્ષની દિશામાં નાનામાં નાનો વિભાગ અનુક્રમે $5 \mathrm{gm}$ અને $0.02 \mathrm{~cm}$ છે. જો $M$ અને $l$ નાં મૂલ્ય અનુક્રમે $500 \mathrm{gm}$ અને $2 \mathrm{~cm}$ હોય તો $Y$ માં પ્રતિશત ત્રૂટિ . . . . . .થશે.
- 9$40^{\circ}\,C$ તાપમાને રહેલા $L$ લંબાઈના સ્ટીલના વાયરને છત સાથે લટકાવેલ છે અને બીજા છેડા પર $m$ દળ લટકાવેલ છે. તેની મૂળ લંબાઈ $L$ પાછી મેળવવા માટે તને $40^{\circ}$ થી $30^{\circ}$ સુધી ઠંડો કરવામાં આવે છે. વાયરની ત્રિજ્યા $1\,mm$, રેખીય ઉષ્મા પ્રસણાંક $10^{-5} /{ }^{\circ}\,C$ અને સ્ટીલનો યંગ મોડ્યુલસ $10^{11}\,N /$ $m ^2$ છે. ધારી લો કે $L \gg $ વ્યાસ છે. $m$ નું મૂલ્ય $kg$ માં ?View Solution
- 10$3.2\,m$ લંબાઈના એક સ્ટીલ ના તાર $\left( Y _{ s }=2.0 \times 10^{11}\,Nm ^{-2}\right)$ અને $4.4\,m$ લંબાઈના એક કોપર તાર $\left( Y _{ c }=1.1 \times 10^{11} Nm ^{-2}\right)$, બંને $1.4\,mm$ ત્રિજ્યા ધરાવતા તારને છેડેથી છેડ જોડવામાં આવેલા છે. જ્યારે તેમને ભાર વડે ખેંચવામાં આવે છે, તો પરિણામી ખેંચાણ $1.4\,mm$ માલૂમ પડે છે. આપેલ ભારનું ન્યૂટનમાં મૂલ્ય. $............$ હશે.($\pi=\frac{22}{7}$ છે)View Solution