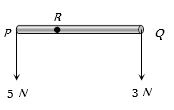
એક વજનદાર $W$ વજન વાળો પાઇપ ને બંને છેડેથી બે માણસે પકડેલી છે . જો એક સમયે એક માણસ તેની પાસેનો છેડો છોડી દે તો બીજા માણસના હાથ પર લાગતું બળ કેટલું થાય ?
Diffcult
d
Let the mass of the rod is \(M\)
Let the mass of the rod is \(M\)
Weight (\(W\)) = \(Mg\)
Initially for the equilibrium \(F + F = Mg\)
\(F = Mg/2\)
When one man withdraws, the torque on the rod
\(\tau = I\alpha = Mg\frac{l}{2}\)
\(\frac{{M{l^2}}}{3}\alpha = Mg\,\frac{l}{2}\) [As \(I = Ml^2/ 3\)]
Angular acceleration \(\alpha = \frac{3}{2}\frac{g}{l}\)and linear acceleration \(a = \frac{l}{2}\alpha = \frac{{3g}}{4}\)
Now if the new normal force at \(A\) is \(F'\) then \(Mg - F' = Ma\)
\(F' = Mg - Ma = Mg - \frac{{3Mg}}{4}\)\( = \frac{{Mg}}{4}\)\( = \frac{W}{4}\).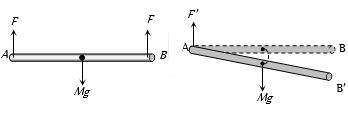
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionકેન્દ્રગામી બળના કારણે ચાકગતિ કરતા કાણનું કોણીય વેગમાન અચળ નીચેના પૈકી ક્યા કારણે હોય છે?
- 2View Solutionકણ નિયમિત વર્તુળમય ગતિ કરે છે. કયાં બિંદુની સાપેક્ષે તેનું કોણીય વેગમાન અચળ રહે છે.
- 3View Solutionએવી પરિસ્થિતિ લો કે જેમાં એક રિંગ, નક્કર નળાકાર અને નક્કર ગોળો સમતલ ઢાળ પરથી સરક્યા વિના ગબડે છે. ધારો કે તેઓ સ્થિર સ્થિમાંથી શરૂઆત કરે છે અને તેમના વ્યાસ સમાન છે.
આ પરિસ્થિતિ માટે યોગ્ય વિધાન કયું છે
- 4View Solutionફલાય વ્હીલ તેની અક્ષ પર અચળ કોણીય વેગથી ચાકગતિ કરે છે. જો અચાનક કોઈ પદાર્થ તેની રીંગ પર ચોટી જાય ત્યારે જડત્વની ચાકમાત્ર શું થશે ?
- 5$PQ$ અક્ષ પર $M$ દળ અને $ R $ ત્રિજ્યાની રિંગની જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
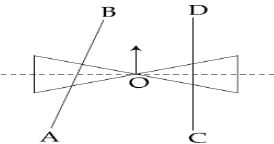
- 6બે શંકુઓને બિંદુ $O$ સાથે જોડીને એક રોલર બનાવવામાં આવેલ છે જેને બે પાટા $AB$ અને $CD$ પર અસંમિત રીતે રાખેલ છે. (જુઓ આકૃત્તિ ), રોલરની અક્ષ $CD$ ને લંબ તથા કેન્દ્ર $O$ એ $AB$ અને $CD$ ને જોડતી રેખાની મધ્યમાં છે. હલકો ધકકો દેતાં રોલર આકૃત્તિમાં બતાવ્યા પ્રમાણે ગતિ કરવાનું શરૂ કરે છે. જયાં કેન્દ્ર $O$ $ CD $ ને સમાંતર ગતિ કરે છે.આમ ગતિ કરતાં રોલરView Solution
- 7બે વર્તૂળાકાર રિંગના દળ અને ત્રિજ્યાઓના ગુણોત્તર અનુક્રમે $1 : 2$ અને $ 2 : 1$ છે. તો જડત્વની ચાકમાત્રાનો ગુણોત્તર કેટલો થશે ?View Solution
- 8View Solutionવર્તૂળાકાર તકતીને સ્પર્શક તકતીના સમતલમાં રહેલી અક્ષ પર ચક્રાવર્તનની ત્રિજ્યા અને વર્તૂળાકાર રિંગને સ્પર્શક રિંગને સમતલમાં રહેલી અક્ષ પર ચક્રાવર્તનની ત્રિજ્યાનો ગુણોત્તર ......... થશે.
- 9$1 \,kg$ દળ અને $10 \,cm$ ત્રિજ્યા વાળો એક પોલો ગોળો તેના વ્યાસને અનુલક્ષીને ભ્રમણ કરવા માટે મુક્ત છે. જો $30 \,N$ નું એક બળ સ્પર્શકીય રીતે તેની પર લગાડવામાં કરવામાં આવે તો તેનો કોણીય પ્રવેગ શું થાય? ( $rad / s ^2$ માં)View Solution
- 10આપેલ તંત્ર માટે પરિણામી બળ $8\ N$ જે $R$ ને સમાંતર હોય તો $PR$ નું મૂલ્ય કેટલું થાય ?View Solution