ગુણાકાર
$\overrightarrow{\mathrm{F}} =\mathrm{q}(\vec{v} \times \overrightarrow{\mathrm{B}})$
$=\mathrm{q} \vec{v} \times\left(\mathrm{B} \hat{i}+\mathrm{B} \hat{j}+\mathrm{B}_{0} \hat{k}\right)$
માં $\mathrm{q}=1,$ $\vec{v}=2 \hat{i}+4 \hat{j}+6 \hat{k}$ અને બળ $\overrightarrow{\mathrm{F}}=4 \hat{i}-20 \hat{j}+12 \hat{k}$
$\vec{B}$નું સંપૂર્ણ સમીકરણ શું હશે?
NEET 2021, Medium
Download our app for free and get started
b
\(\mathrm{F}=\mathrm{q}(\overrightarrow{\mathrm{V}} \times \overrightarrow{\mathrm{B}})\)
\(\mathrm{F}=\mathrm{q}(\overrightarrow{\mathrm{V}} \times \overrightarrow{\mathrm{B}})\)
By check options
\((C)\) \(-6 \hat{i}-6 \hat{j}-8 \hat{k}\)
\(\left|\begin{array}{ccc}\mathrm{i} & \mathrm{j} & \mathrm{k} \\ 2 & 4 & 6 \\ -6 & -6 & -8\end{array}\right|\) \(\overrightarrow{\mathrm{V}} \times \overrightarrow{\mathrm{B}}=\hat{\mathrm{i}}(-32+36)+\hat{\mathrm{j}}(-36+16)+\mathrm{K}(-12+24)\)
\(=4 \hat{i}-20 \hat{j}+12 \hat{k}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એકસમાન ચુંબકીયક્ષેત્ર $\overrightarrow B $ માં એક વિજભારિત કણ $v$ વેગથી ગતિ કરે છે. કણ દ્વારા અનુભવાતું ચુંબકીય બળ કેટલું હશે?View Solution
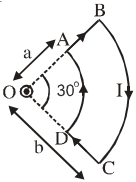
- 2આકૃતિમાં દર્શાવ્યા મુજબ $ABCD$ એ વાહતારનો બનેલો એક બંધ ગાળો છે, જેમાંથી પ્રવાહ $I$ વહે છે. $ABCD$ ને પુસ્તકના પાનાના સમતલમાં રાખેલ છે. $b$ જેટલી ત્રિજ્યાની ચાપ $BC$ તથા $a$ ત્રિજ્યાની ચાપ $DA$ ને બે સુરેખ તાર $AB$ અને $CD$ વડે જોડેલ છે. $AB$ અને $CD$ એ ઉગમબિંદુ પાસે $30^{\circ}$ નો ખૂણો બનાવે છે. પુસ્તકના પાનાને લંબ એવો બીજી એક પાતળો તાર ઉદમબિંદુમાંથી પસાર થાય છે. જેમાં વિદ્યુત પ્રવાહ $I_{1}$ વહે છે.View Solution
બંધગાળા $ABCD$ ને કારણો ઉદગમબિંદુ $O$ પાસે ચુંબકીયક્ષેત્ર $B$ નું મૂલ્ય કેટલું મળે?
- 3ચોરસપ્રવાહ ધારિત લૂપને સમાન ચુંબકીયક્ષેત્રમાં લંબરૂપે મૂકેલ છે. જો એકબાજુ પર લાગતું બળ $\overrightarrow F$ છે. તો બાકીની ત્રણબાજુ પરનું પરીણામી બળ કેટલું થાય?View Solution
- 4View Solutionવિદ્યુત પ્રવાહધારીત ગૂચાળાને ચુંબકીયક્ષેત્રમાં મૂકવામાં આવે છે. તેનું ભ્રમણ એવી રીતે થાય કે જેથી તેનું સમતલ ............
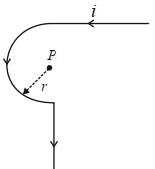
- 5આકૃતિમાં $P$ બિંદુ પર ચુંબકીય ક્ષેત્ર મેળવો. વક્ર ભાગ બે લાંબા સીધા તાર સાથે જોડાયેલ અર્ધવર્તુળ છે.View Solution
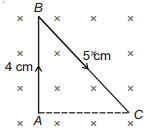
- 6એક એકરૂપ સુવાહક તાર $A B C$ નું દળ $10\,g$ છે. તેમાંથી $2\,A$નો વિદ્યુતપ્રવાહ પસાર થાય છે. તારને એક્સમાન ચુંબકીય ક્ષેત્ર $B=2\,T$ માં રાખેલ છે. તારનો વેગ ........... $ms ^{-2}$ હશે.View Solution
- 7જ્યારે $5\,\Omega$ ના અવરોધને ચલિત ગૂચળાંવાળા ગેલ્વેનોમીટરશતે શંટ તરીકે જોડવામાં આવે છે, ત્યારે તે $250\,mA$ ના પ્રવાહ માટે પૂર્ણ સ્કેલ આવર્તન દર્શાવે છે, જો કે જ્યારે $1050\,\Omega$ નો અવરોધ તેની સાથે શ્રેણીમાં જોડાયેલ હોય, ત્યારે તે $25$ વોલ્ટ માટે પૂર્ણ સ્કેલ આવર્તન આપે છે. ગેલ્વેનોમીટરનો અવરોધ ......... $\Omega$ છે.View Solution
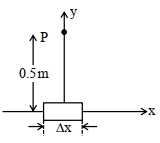
- 8એક ખંડ $\Delta l=\Delta \hat{i}$ ને ઉગમબિંદુ ઉપર મૂકવામાં આવેલ છે. જેમાંથી મોટો પ્રવાહ $I=10 \mathrm{~A}$ પસાર થાય છે. આ $1 \mathrm{~cm}$ લંબાઇના $\Delta x$ ખંડને કારણે $y$-અક્ષ ઉપર $0.5$ અંતરે ચુંબકીય ક્ષેત્ર. . . . . .હશે.View Solution
- 9વિધુતક્ષેત્ર $\vec E = 2\hat i + 3\hat j $ અને ચુંબકીય ક્ષેત્ર $B = 4\hat j + 6\hat k$ માં $m$ દળ અને $q$ વિજભાર ધરાવતો એક કણ રહેલ છે. આ વિજભારીત કણને ઉદગમથી બિંદુ $P(x=1 ; y=1)$ આગળ સીધા પથ પર ખસેડવામાં આવે તો કુલ કાર્ય કેટલું થશે?View Solution
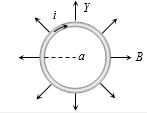
- 10$a $ ત્રિજયાવાળી રીંગના કેન્દ્ર પર $B $ ચુંબકીયક્ષેત્રનું ઉદ્ગમ સ્થાન છે.તે રીંગની ત્રિજયાવર્તી દિશામાં છે.તો રીંગ પર કેટલું બળ લાગશે?View Solution
